|
①这个附录附属于第三编第八章。其中很多地方原想作为国际贸易著作中的一部分附录,这项工作大部分在1869—1873年业已完成。但以后我从事于一项工作,即至少要在抽象理论方面明确地估计国家的需求弹性,及一国的国际贸易对该国的直接总净利得。由于这些特殊情况,现在这个附录,即1879年由私人刊行并流传于国内外经济学者之间的那份手稿,稍加修改重印于此。
本附录中的一些曲线图曾得到我的允许,由潘陶里奥尼教授在他1889年出版的《纯经济学原理》中重印过,这部书已有英译本。在1889年奥斯培兹和莱本所著的影响很大的《物价理论》中曾发现他们自己所画出的曲线图颇类似我的曲线图。参阅莱本在《国民经济杂志》第七卷中的长注解。还可参考《经济学杂志》中埃奇沃思一系列的出色论文,以及坎宁安爵士的《几何政治经济学》。
1.决定曲线形状的条件,这些曲线用来表示国际贸易供求的各种情况及其与国际价值的关系。
把第三编第六章里的表格重印于此,并作为我们研究的起点。对于那里已经解释过的第(2)栏数字何以渐增,和第(4)栏数字何以渐减,不需在此重复解释;但当然既需要以各栏中的数字来解释,也需要以这里的图形来解释。
把下表用图来表示,以沿Ox的距离代表E的包数,以一英寸的尺度代表100,000包;并以沿Oy的距离以同样的尺度代表G的包数。画一称为E曲线的OE代表E愿意贸易的条件。这样,假如P是沿这条曲线运动的一点,而PM永远是垂直于Ox所画的一条线,这样,则当OM连续地代表第(1)栏的数字时,PM即代表第(3)栏中的相应数字。因此,当OM为半英寸,代表E的50,000包时,PM将是十分之二英寸,代表G的20,000包。当P达到A点时,P与Oy的距离将是十分之九英寸,代表E的90,000包;而其与Ox的距离将是稍多于十分之七英寸,代表G的70,000包。

同样,画OG(亦即G曲线)代表G愿意贸易的条件。假如P沿着OG移动,同时画pm永远垂直于Ox,那么,当Om代表第(1)栏的连续数字时,mp即代表第(5)栏的相应数字。当Om为十分之三英寸,代表E的30,000包时,pm将稍多于十分之四英寸,代表G的42,900包。当P达到A点时,Om和pm将各等于OB和AB.OE和OG的交点可称之为均衡点。

2.以图形表示各种正常条件下的国际需求弹性。
定理1.关于OE可能有的形状的每一说明,都有相应的关于OG可能有的形状的同样说明;但是在前一说明中在哪里提到Ox,则在后一说明中即须在哪里提到Oy,反之亦然;当在前一说明中提到水平直线时,则在后一说明中必将提到垂直直线,反之亦然。把有关OE的图形画于薄纸上,朝着光线举起来,把纸的反面对着眼睛,同时令Oy指向右方,就象是一个新的Ox一样,而原来的Ox就成了新的Oy;这样,有关OE的解释即可一字不变地用于OG,尽管OE的形状正常,但可假设OG有各种形状。
OE和OG的形状都不正常所表示的那种情况,是可能出现的,当两个垄断者只彼此进行贸易时就会出现这种情况。关于这种情况,我们在本附录的结尾稍加叙述;但它和国际贸易的实际问题似乎并没有什么关系。现在我们即假定OG的形状为正常。
两种曲线形状变动的可能限度都一样;但在任何特殊情况下,两种曲线可能相差很远。例如,假如E有某些重要输出品对G几乎是不可缺少的东西,而G却没有E所不可缺少的东西,这样则OG在O的附近将为近乎垂直的形状,而OE在O的附近却不会成为近乎水平的形状。这种情况可由第二图来表示。


这个图和第一图一样,代表国际贸易的一般(或正常)情况,在这种情况下,没有一国急切地需要另一国的大部分输入品;同时每一国的需求在接近均衡点的地方都是很富于弹性的。正如第三编第八章中所说过的,这是和现代国际贸易具体问题唯一最有关系的情况。因为事实上一个其输出品为各处所大量需求的国家,只要国际市场上的汇票和其他信用工具能充分起作用,它就可以从别的地方得到同价值的输入品。
但还有另外一种“特殊需求类型”,在这种类型下,一国的外货市场可能如此地不富于弹性,以致中常的供给就会导致供给严重过剩,进一步增加供给就会迫使外国货以递减的收益在市场上出售。第三图的OE形状即表示这种情况。
在实际的正常贸易情况下,OE不可能弯曲到垂直的地步;同时OG也不可能弯曲到水平的地步。我们可用定义的方式把这一点更简单地讲一下,因为它在别的地方还有用处:当曲线的任何一部分呈现这样的方向,使沿它运动的点离开Ox,也离开Oy,则该部分曲线称为正倾斜。相反地,当曲线的任何一部分呈现这样的方向,使沿它运动的点远离Ox,但却接近Oy时,则该部分曲线称为负倾斜。
因此我们得到:
定理2.在正常需求类型(但不是特别需求类型)下,每一条曲线全部都是正倾斜。
在特殊供给类型下,E包的数量被假定为能够迅速而大量地增加,这是由于随着E的输出贸易的增加,它的生产经济有很大发展的缘故。在这种情形下,可以想象G愿意按名义上变动的不利于E的交换比率获得E所增加的数量,因为这种名义上的变动能使它以自己劳动和资本所生产的单位产品来换它愿意得到的货物增加量。但这种情况和实际可能性和实际应用都有很大的出入,因此现在可以暂不提及,留待本附录结尾时研究。
定理3.在正常和特殊需求类型下,假如P是沿OE运动的一点,并画PM垂直于Ox,则PM每有增加,PM对OM的比率以及POM的角度亦随之增加。①因此:
①当E的OA包交换G的AB包时.自然E所得到的输入条件在数学上是由AOB的正切来衡量,而G所得到的条件是由AOB的余切来衡量。
定理4.在正常和特殊类型下,若P是OE上的任何一点,则在OE上O与p之间那部分的每一点,必在OP直线之下;而在OE其余部分的每一点,必在OP直线延长的部分之上。同样,若p是OG上的任何一点,则在OG上O与p之间那一部分的每一点,必在Op线的左边,而在OG其余部分的每一点,必在Op直线延长部分的右边。因此这种曲线不能经过O而割直线两次。
我们晓得,假如G在E出售的包数很少,它将会在有利于G的条件下售出。因此,当PM较小时,PM对OM的比率亦较小;而由O沿OE移动的点最初亦较接近于Ox.同样,由O沿OG移动的点最初亦较接近于Oy,因此:
定理5.在正常和特殊需求类型下,毗连O的OE那一部分必在毗连O的OG那一部分之下。
在已知的条件下,任何在E能售出的G包某一数量的总购买力为已知;同时在该购买力下E能生产的包数亦为已知。因此OE不能象第四图那样向Ox弯曲。因为,假如这样的话,就暗示:G的AB包的售价等于E生产OB包的费用;同时G的CD包(与G的AB包一样)的售价恰等于E生产OD包的费用。但这是不可能的。因此我们得到一个能普遍运用的定理;不象前两个那样依赖于定理3了。
定理6.在任何情形下,OE不能被一个水平线相割两次。同样,OG不能被一个垂直线相割两次。

让我们再来探讨属于正常类型曲线,而不属于特殊类型曲线的一些法则。就正常类型(但不就特殊类型)而言,我们假定,在E每年出售的G包数量每有增加,就增加了出售的全部收入,从而增加了与它交换的E包的输出数量。换言之,若自Oy任何一点N,画出NP与Oy成直角,与OE曲线相遇于P,则ON愈大,NP也愈大。
但在以第四图为代表的特殊类型下,当N沿Oy从O移动时,虽然最初NP随着ON的增加而增加,可是当N达到某一点时(如第四图中的V),曲线和Ox的距离即停止增加而开始减少,从而曲线也向着Ox弯曲。这些情况和OG的相应结果可说明如下:
定理7.在正常类型下,OE不能和同一垂直线相割两次,但在特殊需求类型中则可能。同样,在正常类型下,OG不能和同一水平线相割两次,但在特殊需求类型中则可能。
如A为两曲线的交点(如第一图),则(根据定理4)AE必完全在OA的延长部分之上;而AG必完全在OA的延长部分之右;因此,AE和AG不能再相割。AE也不能与在O和A之间的OG那一部分相割。因为根据定理6,O和A之间的OG那一部分必完全在通过A的垂直线的左边;同时根据定理7,AE必全在该直线的右边。同样,AG不能与位于O与A之间的OE那一部分相割。所以OE和OG除在O和A之外不能相遇。因此我们得出:
定理8.在正常类型下,OE和OG不能相割于一点以上(除O之外);但可以想象,在特殊需求类型下是可能的。
但正常类型是有实际意义的唯一类型,因此对于有关多次相交的讨论,可暂为延缓一下。
假如T在O的左边,则延长的OP线将会再与OE相割,而与定理4有矛盾。因此,纵然这条曲线可以稍向OP弯曲一些(即是说,它有向相反方向弯曲的点),但却不能向后弯回到使P之上任何点的切线与OP平行。象第五图中的点P即切OE两次,但那里T是在O的右边。另一方面,第六图指出一种不可能的OE形状。因为在P附近的反转弯曲达到使T在O左边的程度;同时,画OQQ′平行于PT割OE于Q和Q′;这样则曲线即代表纵然Q′N包小于PM,但E仍愿以较PM不利的条件购买Q′N′包,这种情况是不可能的。因此我们得出:
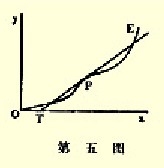

定理9.在正常和特殊的需求情况下,假如在OE上任何一点P的切线PT,割Ox于T,则T必然在O的右边;而在正常情况下,它必然在O和P对Ox垂直线脚的中间。
假如在任何点上,E的需求弹性都是一,则OE在该点必然是垂直的。因为交换比率对它稍许有利多少(由角xOP的增加表示),就会相应地使它的购买增加多少;也就是说,当它得到较有利的交换比率后,他仍将运还和过去一样多的货物。
假如OE属于特殊需求类型,则它可能通过直线弯曲,因此,沿OE向上移动的一点在离开Oy后,又转回来向它移动。假如P在曲线的这一部分,T即会在M的右边;假使T的位置变得无限地离开,因而曲线与xO平行,这就表示没有弹性;即是说,对E有利的比率提高,也不会引诱它增加对G货物的购买。这些考虑提供了下一定理前部分的证据。其后一部分需要用数学方法来说明。
定理10.令OE上任何一点P的切线切Ox于T;假如角OPT是无限小的话,则表示在点P上E的需求弹性是无限大。随着角度的增加,所表示的弹性不断缩减;假如T与M吻合,则弹性等于一。在特殊需求情况下,当T向M的右方移动,则表示弹性缩减为无。需求弹性等于OM除以OT.①
①下面是e的几何证明,e是E的弹求弹性,由曲线中P点表示,等于OM/OT是点P切线切Ox的一点。这个证明同时适用于第七和第八两图,在这两个图中e分别大于或小于一,因此在图中T分别位于M的左边或右边。(见第七图,第八图)
令P,P′为E需求曲线上连续的两点。因此PP′事实上即是P点上的切线,P′R/PM是贸易条件发生微小的实际变化(或如我们普通所说,它所支付的实际价格稍有降低)后,E的购买由OM/PM到OM′/P′M′的相应变化。
3.在人为的简化条件下,用图解来表示一国得自对外贸易的净利益。
第三编第六章第四节中所描述的G在贸易中的剩余,以及那里所指出的限度,现在用第九图来表示。A是G用AB(70,200)包换到E的OB(90,000)包的交换点。在任何方便的距离上画一条固定线DR与Oy平行;这里令OD代表E的100,000包。令OA的延长线切DR于K;并画KH垂直于Oy.
现在DE/FE-DE′/F′E′=DE·F′G-FE·EE′/FE2=(DE-HE)F′G/FE2,
或F′G·DH/FE2;
由于EE′/F′G=HE/FE,
所以EE′·FE=HE·F′G′
因此,I所偿付的价格的相应变化即为
F′G·DH/FE2.JDE/FE=F′G·DH/DE·FE


所以K(即是I购买L货物的相应变化)除以贸易条件的相应变化,
=F′G/FE.JF′G·DH/DE·FE=DE/DH.
微分可以使我们较为简便地得到以上结果。假设(M,N)F的座标,贸易条件由(M,N)到(M+OM,N+ON)的有利于I的相应变动即为
-O/M.NJ/MN=NOM-MON/N2×N/M=ON/MN(M-NO/MN),
PK=ON/NJ.(M-N.OM/ON)ON/MN=M/D/E-MN/ON)=OM/DH.
令DG切DL于D点。通过DL的任何一点F,画DFQ线割RG于F;并延长EF于F′;因此E′成为割ST的一点,E′F′可能等于TQ.这样,L就愿意以它自己的FE包换I的DE包的比率来偿付I的第DE包;亦即是,愿意以它自己的QR包换I的DR包的比率来贸易。因此它在第DE包的地方即得到TQ比率的剩余,这和以E′F′来换I的DR包的比率一样。因此,它的第DE包的剩余由它自已的E′F′包中的第DR部分来表示。
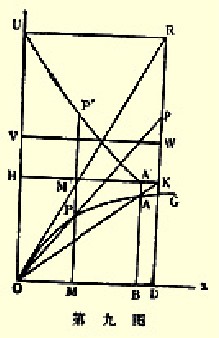
假如F由D开始沿着DL移动,F′即由G对DN的垂直线脚U开始移动,形成一条曲线至V′为止,V′即是WV延长线与ST相交的一点。因此,当F′由U到V′的时候,L得自对外贸易的总剩余或净利得即是E′F′全线中的第DR部分,也就是说,它是USV′面积中的第DR部分。
画XY平行于DM,因此长方形XSTY等于面积USV′。所以相当于一包的单位线XS即是长方形XSTY的第DR部分,同时也是代表我们想要求得的L在贸易中所获得的总(直接)净利得或剩余得。
很明显,点F由D沿DL移动得越快,即切线DG与DM的角度越大,USV′(也就是剩余)也就越大(假定V的位置为已知);同时对DV的距离也就越远。换言之,L需要I的小数量货物越迫切,并能按对它有利而没有大变动的交换率获得I的货物越多,则剩余越大。另一方面,如DL一直很接近于DV,表示L在比以I的DW包交换其自己的WV包的比率要不利得多的条件下,连I的少数货物也不考虑,但它的需求却有这样大的弹性,使它愿在该比率下得到大量货物,那么面积USV′将会变得很小,表示L在贸易中只获得很少的净利得。
求方程的积分(M/NZM/ZN)K=M
在K为常数的假定下,得
NKB1=[MK.
不用说,关于比我们现在所研究的数量小得多或大得多的贸易额的弹性,不可能作出合理的推测,即使这种推测的弹性接近常数。类似的局限性几乎适用于任何经济理论部分的一切数学例证和图解。
假如K无限大,则曲线将变为通过D的直线。假如K=1,则变为M等于常数,假如K=0,则变为N等于常数,与前述结果一致。应该注意,因为ZZN(NM必须为正数,因此MBNZMZN,亦即DH,必须为正数;这样定理9就可直接由定理2推论出来。
再让K′改为代表I愿扩大销售的弹性,而不是愿购买的弹性。这颇类似国内价值中的“供给弹性”(参阅我的《经济学原理》第五编,第十二章,第一节);但这与递减供给和递增供给的影响有特殊关系;假定卖者收到的是对他的边际效用几乎是接近于不变的货币。在I愿意增加售卖量的情况下,决定性因素就将是它换取货物的不断变化的边际效用。这并不暗示,I的输出品有显著的收益递减或收益递增的倾向。现在要求得的结果属于大类型,似乎和现在的问题没有实际联系;但假如把它放在书架上准备以后使用,可能有意想不到的用处。
K′:K=OMM:ONN, PK′=NMZNZMBN
假定K′为常数,来做积分,就得出
NK′=[MK\+1.
假如K′=],我们在上面一样,得到曲线为通过D的直线;假如K′=1,我们就得到以DN为轴的抛物线;假如K′=0,我们就得到平行于DN的直线,这些结果本身就是合理的。
4.在某种和实际贸易的正常情况没有很大出入的前提下国际供求均衡的稳定性。
把相当于I和L之间任何时候的贸易实际情况的那一点定一名称,将会有许多方便。假如在任何时期内,I输出DE包以换取L的D^包,画出EF和^F,分别与DM和DN成直角,相交于F;则F即为该时期内的交换指数。
我们可以假定开始时交换指数不是在V;一些外部干扰力量,如战争或歉收,使交换指数处于这样的位置,在这一位置,与交换指数相应的贸易不处于均衡状态。我们可以研究支配指数变化的力量。
定理6说,DI不能与经过F的水平线相割两次,DL也不能与经过F的垂直线相割两次。于是我们有下述定义:
说一个点是在DI的右边或左边,要以此点究竟是在DI和经过此点所作的水平直线交点的右边抑左边为断;同样,说一个点是在DL的上边或下边,要以此点究竟是在DL和经过此点所作的垂直线交点的上边抑下边为断。
大部分有关国外贸易的纯理论可由上述定理和下述定理推论出来。
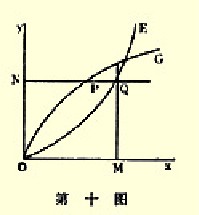

定理11.若任何时候交换指数是在DI的右边,则它将趋于向左移动;若它在DI的左边,则它将趋于向右移动。同样,若任何时候交换指数在DL的上边,则它将趋于向下移动;若它在DL的下边,则它将趋于向上移动。
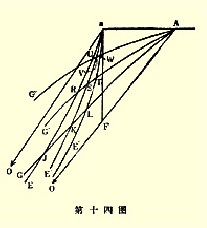
为了证明,让交换点F在DI的左边,如第十图,并让^F延长与DI相割于_.那么,因为_是DI上的一点,所以L每年得以在I销售出D^包以换取I生产和输出^_包的手段。但在当时,L正把D^包输入于I,而I只有^F包输出和它交换。结果是,这种贸易提供了特别高的利润;同时,由于竞争假定是自由的,I的输出包数将会增加。因此,当交换指数在DI的左边时,它将趋于向右移动。所以交换指数若在^_延长段的F′,就表明I每年以^F′的比率输出,以换取L的D^包数;此数在I只能卖得生产和输出^_包的费用,结果是,I输出的包数将趋于减少,即是说,当交换点在DI的右边时,它将趋于向左移动。同样的证明可以用于有关DL的第二部分定理。①
①因此,交换指数的运动在任何方面,都与一个自由移动的物质微粒的运动相似,该物质微粒在各种力量的作用下不断向OE和OG移动。假定OE为一坚硬的金属丝,它只能在水平方向发生吸引力,并且依照书中的定义,当微粒位于OE的左边时,吸引力总是趋向于右边,反之亦然。同样,假定OG为一坚硬的金属丝,它只能在垂直方向发生吸引力,而且依照书中定义,当微粒位于OG的下边时,吸引力总是趋向于上边,反之亦然。这样,微粒的运动就将与我们的交换指数的运动完全一样,所以我们若对这些水平的和垂直的力量给以任何特殊法则,我们就会对交换指数的运动得到一个微分方程。
我们可以把DI和DL相交一点的均衡视为稳定的,若当交换指数碰到该点附近的任何一条曲线时,作用于该指数的力量将使它沿着该线摇摆着趋向于该点。在其他情形下,均衡是不稳定的。
很明显,假如DI和DL属于正常类型,则它们彼此(除D之外)只能相交于一点;该点即代表稳定均衡(见第十附图中的箭头)。若曲线能属于别的类型,则可以相交几次。
5.I和L的各种不同程度的需求弹性,分别影响它们之间对贸易条件的改变,这种改变是由于I对L商品的需求增加而引起的,现以放大的图解来说明前面对这些影响的研究。
下一步我们要解释第三编第八章第一节中提出的问题,我们已经晓得该曲线是属于正常类型;因此,它们不能与同一垂直线或同一水平线相割两次。对于特殊类型将延缓到第8、第9节论述。
我们假定I对L货物的需求增加;因此DI移至新位置DI′。在DI上的任何一点F画FQE、FF′及F′E′如第十一图。这样,F′必位于F的右边,而Q必位于F的下边。因为I用FE(或F′E′)包向L交换的DE′数量大于DE;同时它用自己的DE向L交换的QE数量小于DE.这指出表示改变的两种方法:我们可以说DI是向右移动,或是向下移动。如果DI不属于正常类型,它就有可能与同一垂直线相割一次以上,尽管在任何情形下,都不能与同一水平线相割一次以上;在这种情况下,我们可以说,I的需求增加使DI向右移动。
为了使概念明确,我们可以假设,由于I的人口增加,或由于I取消了对L进口货的关税,任何一定数量的L包所能支配的I包数增加了六分之一,也就是DE′等于DE的六分之七。
这种情况在第十一图中大体上有所说明,该图中的DI和DL是重印第一图的。V即是原来的均衡位置。画水平线`Va通过V,割DN于`;Va是`V的六分之一。那么,在上一节的假设下:由于I的需求增加,所以它用比原来多六分之一的包数来换原来L的均衡包数WV,a是I新需求曲线上的一点。令DI′割DL于V′。那么,V′就是新的均衡位置。假如I的新曲线的一般形状和老曲线一样的话,则V′必然和图上所指的位置大体一致。
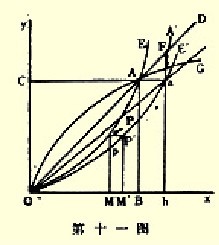

但假如我们除了假定两条曲线都是一般的或正常的类型,并相交于V之外,并没有更假定有关DI或DL的形状;同时,假如我们假定DI′只是象DI那种一般的类型并通过a的话,那么我们对于V′的位置所能够知道的只是它位于面积RbaZ之内;R和Z是DV和Da直线延长段上的点,而b是通过a的垂直线割DR的一点。因为,既然DI′和DL属于正常类型,V′就不能位于a的左边,也不能位于V的下边。又既然它是DI′上较a距离D更远的一点,它就必须位于Da之上;又既然它是DL上较V距离D更远的一点,它就必须位于DR之下。
为了详细研究I和L的需求弹性对V′的位置所产生的影响,需要占用较大的篇幅。第十二图中的RVaZ是把第十一图以放大的尺寸重印于此。我们可以严格地随着文中所述的次序来观察。字母R、b、V、a、Z和第十一图中所代表的意义一样;所以RV和Za如果延长到图外,就会相交于D.VL、VL′和VLc是L需求曲线的连续,各代表弹性的大、中、小;同时aI、3I′和aIc是新情况下I需求曲线的同样的连续。
让我们先讨论当L的需求很富于弹性时,以DL表示的一组结果。它们都指出L产品的输出有很大的增加,因为d、T和e都远在V的上边,而角eDM、TDM甚至dDM并不比VDM小许多;这表明,I可以得到L的增加的供给而不致大大改变交换比率。因此,整个说来,L的较大需求弹性是对这组结果的主要影响。
第二组结果由I的新需求曲线的三个交叉位置表示,以DL′代表L需求的中等弹性。G、f和H在同一方向的差别正和d、T和e的差别一样,只是相差的数量较小而已。整个说来,它们和上面第一组结果不同的地方是比较密集。I的需求弹性的变动,对于交换比率所产生的影响较上面的情况为大,但它对L的供给的影响却比以前小。因此在这里,L的需求性质的影响虽不象上面那样显著,但仍然是主要的。
另一方面,在最后一组结果中,L的需求性质是最主要的因素。因为I的新需求曲线上的三个交叉位置U、X和Y及代表L方面很不富需求弹性的一条曲线,它们的位置很接近,并都接近于a.其中每一个都指出,I所得到L的货物只有很少的增加,但让出较旧均衡多六分之七以上的输出品,所以必须忍受较旧时远为不利的交换比率。
自然,在d、T、e的交换比率,对I说来是有利的上行次序,对L说来是不利的上行次序;在G、f、H和U、X、Y,在Y、H、e和X、f、T以及在U、G、d等位置的交换比率都是一样。在Y、f和d的交换比率大致相等;在H和T,以及X和G的位置也是一样。
6.以图解来研究I和L各种不同程度的需水弹性对它们之间贸易条件变化的影响,这种变化是由于I对L商品需求减少而引起的。
现在我们用图解的方法来解释上节里的问题。令F为DI上的任何一点;画FE垂直于DM;在DE上取一点E′,使DE′=5/6DE,并画E′F′垂直线等于EF;这样,F′即是I的新需求曲线DI′上的一点。因为若L以FE包提供于I市场,就将要买I的DE包;但其中EE′被I政府拿去,因此将只有DE′可送还给L.令DI′割DL于V′;这样,V′即是新的均衡位置;同时以Va代表租税,a是在通过V的一条水平线上与I′相交的一点。

画DV和Da两条直线,ab垂直于DV;这样,V′就必位于直线三角形Dab之内。因为和上面的情形一样,由于DL是属于正常类型,所以VV′必位于DVa角之内;又由于DI′是属于正常类型,所以aV′也必位于Dab角之内。
对I有利的贸易条件的变化,以VDV′角来表示。我们必须研究,在租税Va为已知的情况下,使这个角度变大的条件是什么。很明显(若我们先把DI′的形状作为已知),V′Va角度越小,也就是在V附近的L的需求弹性越小,VDV′角越大。若我们再把DL的形状作为已知,那么,VaV′角越大,也就是,I的需求弹性越大,VDV′角就越大。把两种结果结合起来,如租税的数额为已知,L的需求弹性越小,I的需求弹性越大,交换比率向有利于I的方向变化的幅度就越大。
进一步研究时,我们就会晓得这些条件中的第一部分较之第二部分一般说来更为重要。为了这个目的,我们把第十三图中DVa的上一部分割下来,用第十四图的放大尺寸来表示。
详细研究一下我们就会注意到,当L的需求很富于弹性时,VL即是L曲线上的一部分。假定它的需求各有大、中、小三种弹性,则它将与I新曲线上的aI、aI′和aIc相交。点d代表I和L的输出大大收缩,尽管贸易条件变动很小;同时租税几乎都由I来负担。T和e代表贸易只有很小的收缩,转嫁给L的租税负担则略有减少。
在G、f和H所代表的每一种情况下,租税负担要大得多,贸易的收缩要小得多;G、f和H是中等弹性的L曲线和不同弹性I曲线的交点。
第三组交点U、X和Y,是弹性很小的L曲线和不同弹性I曲线的交点,它们指出L的输出几乎没有收缩,但I的输出却收缩了六分之一以上;在各种情况下,I的全部租税负担几乎都转嫁给了L.
在d、T和e的交换比率,对I的利益来说是下降的次序,G、f和H,以及U、X、Y等也都一样。
L的输出对U、X、Y组内每一数目几乎都一样;在第二组G、f、H的三个数目之间。L输出的差别不很大。I的输出在每一情况下都收缩六分之一以上,但除在其需求很富于弹性的时候外,不会远远超过六分之一。
下一步我们可以研究一个抽象问题,即假如对I的输入品课税,其全部税收都用在L的货物上面时,这对交换比率有什么影响;或者换一种说法,若租税以实物征收,所征收的全部L货物由政府保留,这对交换比率会发生什么影响。在这两种情况下都假定,政府对L货物的消费完全不起它在I的私人消费者手中所起的作用。
和上面一样,令租税数额,比如说,为存于仓库中的输入品价值的六分之一;但现在(如第十五图所示)在FE上取一点G,使FG=1/6FE.那么,假如由L输入FE包,则政府即会拿去其中的FG,只留GE供私人消费。画GQ水平线切DI于Q,并画QFc垂直线割通过Q的水平线于Fc,这样则Fc将是在I的新需求曲线DIc上相当于F的一点。
因为QEc代表由L输入I的FE包中的六分之五,它是将要投入普通市场上的;DI曲线指出它们是能够交换I的DEc包的。由于为了使私人消费者能得到L的QEc包,QFc必须直接或间接无偿地交给它的政府;所以I只准备提供它的DEc包以换取L的FcEc包。很明显,Fc必位于F的左边。但如果象第七十一图那样,画出DI′曲线,代表课征六分之一的I输入税之后I的需求(税收用于买I的货物);如F′是DI′上相当于F的一点,则Fc必然位于F′的右边。换言之,DIc位于DI和DI′之间,因此,现在所讨论的租税对贸易条件所产生的影响,正同那种较小的税额一样,其收入一如往常用在I的货物上面①。


①这里可以对Pc必然位于P和P′之间这一明显事实,再添上一种证明。在Ox上取M′,使OM′=六分之五OM;再垂直地画M′P′交PPc于P′。这样,P′即位于OE上面;并且
FF′=1/6DE=1/6FEgahDFE,
同时FF′′=FGgahQFG=1/6FEgahQFE.
但根据定理9,QFE角必小于DFE角;因此FFc必小于FF′。
在这里还应该简单提一下这种情况,在这种情况下,曲线之一,也就是G的曲线,属于特殊需求类型,如第十六图所示。假定E对其输入和输出征收重税,对自己毫无损失,反而大大有利(这种税重得足以使其需求曲线从OE移至OE′),则贸易将在A点处于均衡状态。这就将使G以A′H′包(约为AH的三分之四)换E0的OH′包(约为OH的三分之二);这样就使E的每一百包可换两倍于过去的G包。这种收益被分配于E政府和E的G货物消费者之间,而E的财政部在收税上并没有很大的麻烦。
7.用图解方法来说明E征收的输入税对G的损害(假定这种输入税已达到能减少G的一部分很不富于弹性的需求的地步),并用图解方法来说明G如何利用E欠它的债务来抵制E.
现在我们可以用图解方法来阐述第三编第八章第三节提出的那个一般意见,即:尽管G急切需要E的一部分输入,但仍可抵制E对它的输入(或输出)课征重税;假定E对其输入品的需求一直富于弹性。


第十七图表示G对极小数量商品的需求没有弹性;第十八图表示G对较小数量的需求属于特殊类型;在每一曲线中,邻近于正常均衡位置的需求都是富于弹性的。
在每一曲线中,如E按贸易价值课征轻微的(输入或输出)一般税,而不把它作为政府增加消费G货物的手段,则E的曲线即由OE移至OE′,而均衡点由A移至A′;同时,课征很重的同一类税,则将使E的曲线移至OEc,均衡点移至Ac.但第一种变动对于交换比率只有比较小的影响,因为AOH′角在每一图中都只比AOH角稍大一点。但重税则使交换比率变动得很不利于G,因为在第十七图中,AcOHc角要比AOH角大得多;而在第十八图中尤其大。
但假如E每年都必须向G交付一定数量的货物(以OL表示),作为G在E各种投资的利息和利润,则位置将会有很大的变动。因为这样一来,E的一切需求曲线,如OE、OE′和OEc都要向右移动相当于一个OL的水平距离;也就是说,它们将都由L开始而不由O开始,并按照由O开始的OE、OE′和OEc的同样路线各自由L开始。
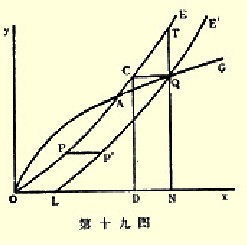
证明如下:令P为E需求曲线上的任何一点(无论它是在原来的位置,还是由于较轻或较重的进口税而移向左方,都没有关系);由P向外画水平线PP′,并等于OL,如第十九图所示;在这种情况下,P的轨迹即是E的综合需求曲线LE′。令它切OG于Q,Q即是新的均衡点。因为画QC水平线与OE相交,并画CD和QN垂直于Ox,那么,由于Q是在OG曲线上,由E输出的ON包即可在G市场上售出以换回G的QN包;又由于C是在OE曲线上,因此G的CD包即可在E市场上售出以换回E的OD包;同时E应付给G的利息等收入则以多交付的DN包来作抵。因此当G由E获得ON包以换取它的ON包时,贸易即达到了均衡。假如它没有DN(或OL)包那样多的利息作为防御力量的话,它就必须偿付NT包;T是QN延长线交于OE的一点。
现在回到第十七和第十八图,我们延长NQ交OE于T点,N′Q′交OE′于T′点;但无论我们延长到多么远,NcQc总不能和OEc相割。这些结果表明,G能从E取得OL包而不需以它自己的货物来交换,这就使它能以比在E不征进口税和征很轻的进口税的情况下对自己有利得多的比率,得到E的更多商品。当E对它的输入课征很重的税时,这种保护使G得到的E商品量,比E愿意在这种情况下消费G的商品量大,即使G提供的交换比率大大不利于它自己。除固定的支付以外,G以不高的价格得到了OHc这样一大批E国商品。
8.单独研究资本和劳动在生产一个国家的输出品中的递增收益倾向有一些障碍。
本附录剩下的部分与一国对外贸易中实际存在的问题没有直接关系,而是讨论由李嘉图和穆勒提出并发展的那种关于假想国际贸易的一般理论。虽然这部分内容只可直接应用于两个孤立国家之间在理论上可以想象的贸易问题,但把它改换成另一种形式后,也可应用于两个团体之间的任何一种交易,条件是它们之中在这种交易中没有一个遇到外部竞争。
一个国家如果不首先以较大的规模发展国内消费工业,它就决不可能在出口工业方面居于领导地位。但是,输出贸易可以为从事大规模贸易提供极为有利的条件;大规模贸易反过来又促进大规模的制造业。因此讨论一国制造品输出的增加可能影响其对外贸易数量,从而又影响其条件,不是不合理的。特别是英国的输出贸易一直从容而不断地影响工业中的技术和经济。正如亚当·斯密所说,国外贸易的一种主要利益是“由于它,国内市场的狭隘性就不会妨碍任何技术和制造部门中的分工达到最完善的地步。”
这些事实的提出,并不能证明在讨论特殊供给情况时所作的假设是有根据的。要证实那种假设,就必须向人们表明,生产成本的急剧下降起源于输出品的增产,而和国内对大部分输出品需求的增加所可能产生的影响完全无关。这在任何大工业国的一般输出中从未发生过,显然也不可能发生。
而且,我们已一再指出,在经济学中,每一事件会永久性地改变未来事件发生的条件。在某种限度内,物质世界的情况也是如此,只不过程度没有那样大罢了。作用于钟摆的力量,几乎不受钟摆摇动的影响,而物质世界中的其他许多运动则完全是过去运动的翻版。但在精神世界中所发生的每一大运动,纵然不致改变以后运动力量的性质,但也会改变其大小。经济力量,就其依赖于人类的习惯和感情、知识和工艺而言,是属于精神世界的。
例如,当任何偶然事件增加了俄国所消费的任何一种英国商品的数量时,就俄国消费者对英国商品的熟悉而言,便留下了永久的影响,并在各方面引起了需求情况的永久改变。如果情况的变化改变了英国商品在俄国出售后的收入并进而改变了俄国每年输出的商品数量,则俄国的需求曲线形状就必然有所改变。结果是,交换指数的每一变动必然使曲线形状发生某种变化,从而也就使决定以后运动的力量发生某种变化。若曲线属于正常需求类型或特殊需求类型,则这种必需的变动大概不十分广泛。无论如何,曲线的一般性质很少被改变;虽则均衡位置可能稍有移动,但根据曲线形状保持刚性和不变这一假设而作的推论的要旨,将不会因此而失效。
但假如任何一条曲线属于特殊供给曲线,则这些推论将往往失效。因为,为了输出而生产的棉布数量增加,会带来大规模生产的经济效果。这种经济效果一经被获得,就不容易再丧失。机械工具、分工以及运输组织等一旦发生作用,就不会被人轻易放弃。某一行业所使用的资本和熟练劳动,当它们所生产的产品的需求减少时,固然会贬值,但它们却不会很快地转用于其他行业。所以它们的竞争会暂时阻止需求的减少使商品价格上涨。①
①本书作者在《经济学原理》的附录H中曾主张,虽然在任何市场内,一种商品的需求曲线可能和该商品在收益递增倾向下的供给曲线相交数次,但根据这些交点所作的某些推论,由于以下事实而失效:若供给点沿着曲线向前向下移动,随后又不得不转回去的话,它就不会再沿着老曲线转而向上;它将在老曲线下面形成一条新的曲线。
9.如果作以下极端的假设,即两个假想的国家,每国只和对方从事贸易,对其少量商品的需水很迫切,而对其大量商品并无用处,那么在它们之间就可能有几个稳定和不稳定的相互交替的均衡位置。
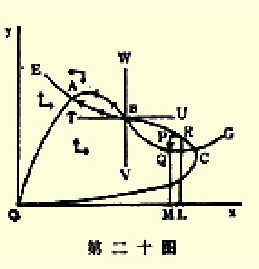
若OE和OG都属于这种特殊需求类型,它们就可能彼此相割三次(或任何其他单数),O不算在内。从O起无论向任何方向最先达到的交点将是稳定的,第二是不稳定的,第三又是稳定的,余类推。从第二十图(相当于第十图)中所画的箭头最容易看出这一种情况。这些箭头指出,O是一个不稳定均衡点,A是稳定的,B是不稳定的,而C又是稳定的。由观察中看得很明显,为了两条曲线都能相割一次以上(不算O),它们都必须属于特殊需求类型;即是说,除非其中的一条能弯曲回去以便通过O和同一直线相割。但一种简单的几何证明可以即刻由定理6推出。
对于大部分目的,以上的简短说明已够用了。但为了完整起见,还可增加一条正式的定理,即是:OE和OG相交的每一点上的均衡,都是稳定的,除开那些点,在那里两曲线都是正倾斜,但OG较OE更垂直;并除开那些点,在那里两曲线都是负倾斜,但OG较OE更垂直。
这种情况可从第二十一图看出,在那里D是OE和OG的任何一点的交点。画TDU和VDW水平直线和垂直线如图所示。

首先,令OE在D点上为正倾斜;让它以直线eDE的方向指向D.于是均衡将成为稳定,只要OG或是(1)在D点上为正倾斜,但与垂直线形成一个比eDE大的角度(例如以gDG的方向指向D);或是(2)负倾斜,例如以g′DG′的方向指向D;或者,换言之,只要OG位于。eDW、EDV角度以内。
因为,假定交换指数恰在D的下面碰着OE,那么,无论OG位于gD或g′D方向,它必在OG的下面;因为eD位于gD和g′D二者之下,所以它必然被吸引向上去。因此,在eD上的箭头必指向D.所以可以证明,在DE上的箭头指向D,在gD和DG、在g′D和DG上的箭头也指向D.这证明,在所述的情况下,D是一个稳定的均衡点。
也可用完全同样的方式来证明,在D的均衡将是不稳定的,如果,虽OE以eDE的方向位于D,但OG是正倾斜,并与垂直线形成一个比eDE小的角度,因而位于eDV、WDE角度内。
也可用同样的方式来证明,若OE在D是负倾斜,在D的均衡就是稳定的,除非OG在D也是负倾斜,并较OE更垂直;这就完成了这个定理的证明。
自然,没有任何事物能阻止OE或OG接近联接A和C的那条直线。在那种情况下,它们可能以任何奇数的次数在两点之间彼此相割;一种小的扰乱就足以使交换率移动,离开一个稳定均衡位置到达下一个位置。但这一切都是想象的游戏而不是以目击的事实为根据。因为在大部分表格中都假定每一国家的总需求弹性小于一,平均需求弹性小于二分之一。在现实世界中从未发生过这种情况;它不是不可以想象的,但却是绝对不可能的。①
在图中所表示的情况下,两个稳定均衡位置的距离很远;假如交换比率在其中之一的A上不变,则当遇到轻微的扰乱时,它就在A的附近摆动。除非遇到某种猛烈的扰乱把它抛掷到远离于A的地方,它是不能移动到C的。若它是这样地被抛掷出去,则它是否又回到A或移动到C,要看驱使它走向各种方向的相对力量大小如何;而这将主要取决于抛掷它离开原来位置的那种动乱的性质和持久性②。
①参照第六和第八图,我们就可看到,假如AC和Ox及Oy都成45°角,则在某一点上这一点离两轴的距离都一样,它所代表的每一曲线的弹性即为1/2.若某一点离Ox轴为离Oy轴的三倍距离,则G的需求弹性为3/4,E为1/4.若AC和Ox成其他的角度,则一条曲线的弹性大于上面的,另一条曲线小于上面的。
②与定理11有关的那个比喻:即在两条坚硬金属丝吸引下运动的微粒,有助于使这个问题形象化。
在支配这些力量的强度的各种因素中,最主要的自然是在输出大增加时难于找到足够的劳动和资本,或另一方面由于输出贸易收缩而被解雇的劳动和资本又急切地需要就业。固然它们都特别易于遭受所述的那种扰乱的影响,但是除了受这样的影响之外,必须估计它们的全部力量;可是不能计算两次。①
①但穆勒想在下面的事实里找到一把人们没有发现的钥匙,来解决那个否则就不能解决的“比率不确定”问题:一个国家的输入品常常代替一定数量的本国制造的类似货物;一国所能制造的输出品的数量决定于用来制造这种货物的劳动和资本的数量。穆勒在这里似乎搞错了一些事实。一国输入的货物,在性质上一般都不同于如果没有国外贸易就要自己供应的货物。制造输出品所需要的资本和劳动大都取自制造国内货物和劳务的资本和劳动,它们在性质上既不属于输入品,也不属于输出品。因此并没有象穆勒所说的那样一把钥匙。
而且,穆勒是要确定,在一切可能的均衡位置中,两国之间的贸易将处于哪种均衡位置,在其中每一国家里,“廉价产品增加多少,消费量也就相应增加多少”;这即是说,每一国的需求弹性都等于一。无论交换比率怎样,E都愿意输出一定数量的商品,例如第二十二图的OV,也就是说,它的输出将是无条件地等于OV数量。同样,G的输出将会无条件地达到OW数量。也就是如我们所知,E输出它的OV货物于G,G又以OW货物为报酬;问题完全没有解决。
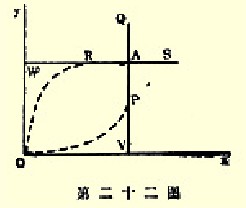
自然,这种情况是不可能出现的。可以想象,E的需求曲线全长中的一部分可能是一垂直线,但却不是全部如此。因为如果它能象AV那样,那就意味着,E愿意以OV的货物来交换G的无限小的数量。
10.在特殊供给情况下,一国的输出往往呈现出强烈的收益递增倾向。由于静态方法不适用于表现这种倾向,因而表示特殊供给情况的图解没有实际意义。
特殊供给情况,业已定义为这样一种情况,在这种情况下,其中一个国家(我们假定为G)的出口工业的大规模生产的经济效果因对其出口的需求增加而增加,这会大大增加其劳动和资本所生产的包数(也就是其劳动和资本的单位产品),致使别的国家(E)愿意按名义上(虽然不是实际上)不利于自己的交换比率得到增加的数量。即是说,使E的曲线属于特殊供给类型的原因,根据这个定义,不是它自己的工业条件特殊,而是它所进行贸易的那个市场上的工业条件特殊。结果,当点P由O沿着OE运动时,xOP角就不一定象在正常情况和特殊需求情况下那样不断增大。即是说,定理3不适用于这种情况,定理4、5和9也是如此。在这种情况下,通过O的直线可能割曲线一次以上;邻近P的那部分OE曲线可能位于OG的相应部分之上,切OE的线可能割Ox于O的左边。纵然曲线属于这种类型,但第三节有关一国贸易净收益的论点仍然有效;但如别国的曲线也是这样的话,就无效用了。另一方面,定理6和12中关于特殊供给的论点仍然有效。
纵然OG属于正常类型,如第二十三图所示,但如OE属于特殊供给类型的话,则它仍可能割OG几次。然而,如果OG也属于一种特殊供给曲线,则两条线将如嬉戏似的有更多彼此相交的机会。若OE在O的附近位于OG之上,O即是稳定均衡点,那么以后的第一个交点A一定是不稳定的;其以后的不稳定点必然是单数的交点,而不是双数,如象A是稳定点的那种较为自然的情况那样。
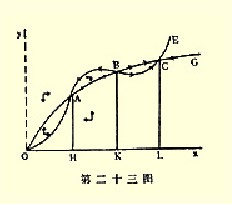
假如OG曲线全部属于特殊需求类型,而OE全部属于特殊供给类型的话,除非O是不稳定点,不然它们就很难相割两次。但假如E对G货物的增加量(不是对G的劳动和资本的单位产品)的需求弹性远远小于一,则会产生很错综复杂的结果;因此,如果G的供给正常,OE就会属于特殊需求类型。①
①假如衡量单位是一国输出货物的某种人为的平均数量,而不是该国劳动和资本的单位产品,则使G由于产品输出的需求增加,从而输出工业成本显著下降的那种特殊供给情况,将会影响G的曲线形状,而不影响E的曲线形状。因此将是OG而不是OE属于特殊供给类型;但这种代替一旦形成,则正文中有关许多交点的推论就可能完全运用,图解仍保持不变。
关于这种特殊情况的原稿是用以研究假想中的贸易的。在这种贸易中,大规模生产的经济,如此强烈而迅速地发生作用,以致OE和OG可能出现某种奇异的形状。但在该稿写好后的这许多年中,我发现它并没有什么用处,所以这里把它删去。
11.简要论述在一切可以想象的相互供求条件下,只彼此贸易的两国中,一国征收普通进口税所产生的奇特结果。
我们现在要研究在曲线不限于正常类型的情形下,征收麻布输入于E的进口税,或使E曲线推向左方的其他变动所可能产生的影响。但在未研究之前,可以很方便地通过观察曲线图获得关于这些结果的一般概念。
在第二十四图中,两条曲线都属于第一类型,在第二十五图中E曲线属于第二类型。②E曲线由OE位置移动至OE′位置相当于课征轻税,移动至OEc位置相当于课征较重的税。
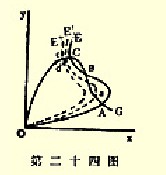


②从此以后,“第一类型”作为“特殊需求类型”的简称,“第二类型”作为“特殊供给类型”的简称。
先让我们研究,E曲线由OE位置推向OE′位置所产生的结果。这样,两个图中的交换指数,如果改变前在A,则改变后即移至a;如果改变前在C,改变后即移至c.注意在两图中a较A更接近Oy,c较C更接近Oy.这即是说,在每一图中,在交换指数由A到a或由C到c的四种情况中,无论在哪种情况下,棉布的输出量都减少。麻布输入E的数量,在四种情况中的三种情况下都减少,只有在第二十四图中交换指数由A移至a的情况下,麻布输入E的数量才增加。同样,假如画直线由O至A、a、C、c,则在两图中cOx角皆大于COx角,aOx角皆大于AOx角。这即是说,在四种情况中的每一种情况下,交换比率都向有利于E的方向移动。
在以上的情况中,最使人感兴趣的是第二十四图中交换指数由A移至a的情况。因为在这种情况下,征税会使交换比率变得对E非常有利,使它能以减少的棉布量来换得增加的麻布量。但这种类型的更显著的结果是当E曲线进一步向左移达到OEc位置的时候。因为这样,交换指数就会移至d,E将能以不到原数量一半的棉布来换得比原来多一倍以上的麻布。
给第二十六图中的几条曲线以一种特殊的解释,我们可以使它们更适合于某些重要实际问题的具体情况。在这里,E可以认为是代表英国,G代表德国。
让我们不用沿Ox的距离来衡量代表E输出于G的全部货物——棉布,而用这个距离只来衡量E输出的一种商品,例如煤。
OE不能再称为E的需求曲线,而可称为E的煤输出曲线;OG现在可称为G对煤的需求曲线。OE现在将成为这样一条曲线:假如在OE上取任何一点P,并画PM垂直于Ox,OM即代表英国各年愿输出的煤数量以交换PM所代表的德国商品数量。因此,OG现在将成为这样一条曲线,假如在OG上取任何一点,并画pm垂直于Ox,pm即代表德国每年愿输出的商品量以交换Om所代表的英国煤炭数量。
现代史①告诉我们,德国对煤的需求曲线可能是象第二十六图所画出的那种样子。但英国的煤输出曲线却不可能属于第一类型;它不能弯回去接近于Oy.因为在德国出售英国煤的收入用以购买德国商品的数量不会很大,而且这种数量事实上也不会增加到足以使这些商品的总供给充斥英国市场,以致使这些商品的售价大幅度下跌。
①[1921年附注。这系指1873年达到顶峰的那些事件。写本文时(约在1871年),由于一时疏忽,我错误地用货币来衡量进出口价值;后来的物价崩溃,证明这种做法是很危险的。但似乎最好还是把这一段按原样保留下来。]
在图上我们看出,如果任何原因使英国煤的输出曲线向左移,也就是由OE移向OE′,这一原因也就会使交换指数由A移至a,也就是使英国可以用比过去少的煤来换得比过去多的德国商品。但是,正如前面指出的,虽然英国能够对煤的输出课征特别输出税以达到这种结果,但却不能用课征德国商品的进口税来达到目的。因为德国对英国商品的需求一般是属于正常类型。虽然德国不会轻易放弃英国煤炭,但却有许多别的商品只有按现在的交换比率它才肯买;若英国想用课征进口税的办法来改变交换比率,使之对自己有利,它就会从自己的生产者或别国的生产者那里去买。同样,欧洲各国对高级美棉的需求曲线,也是属于第二十六图的OG所代表的那种性质。因此,美国可以通过对这种产物课征特殊的出口税得到暂时的收益,但只要美国输出的大部分棉花及其他货物遇到别国对手的激烈竞争,美国的进口税负担就不会主要落在欧洲各国的身上。
符合于第二十六图曲线的一国对别国小额贸易的情况,虽然不是不重要,但却不是很普遍的。不过任何一个工业团体对社会其余部分贸易的情况可经常以这种曲线来代表。例如,某时某地社会上需求新房屋的情况,或许很符合图中的OG曲线。建筑商愿意出售劳务的那种情况可用OE来代表;工会以具体条文写出的要求可以正确地解释为他们确实能够把曲线向左推移到OE′的位置。这样,他们就以他们自己的减少的劳动,来获得社会上财富增加的数量。
第二十五图中的OEc位置,使我们感到兴趣,也是与某些工业团体的商业情况有关,而不仅是与两国间的贸易有关。〔假如这个图中的交换指数为a,而英国的曲线推到OEc的位置,则会得到交换指数离开d,贸易接近毁灭的奇特结果。〕
在本节中,OE′曲线被认为是E课征麻布输入税之后E的需求曲线所处的位置;或是发生如下事件后E的需求曲线所处的位置,这种事件使E对麻布的需求减少并把E曲线推向左方,但却不改变G曲线的位置。这类事件以下将简称之为“情况的变化”。
情况的变化将使棉布输往德国的数量减少。换言之,假如交换指数在情况变化前是以A为均衡点,情况变化后指数的均衡点必然在A的左边。当英国曲线在OE′位置时,交换指数就被认为在A.从这个时候起,作用于指数的力量将趋向于使它向右或向左移动,这要看它是在OE′的左边还是右边。但根据构造,A是在OE′的右边。因此,假如交换指数在情况变化时在A,则情况变化后它将沿着GO移向左边。
在以上的推论中,我们并没有假定在A的交点是稳定的均衡点。因此,其结果是:假如OG同OE和OE′有许多交点,则这两组交点将沿着OG一对一对地分布。这即是,假如我们由OG和OE的任何一个交点沿OG到其他交点,我们必须经过OG和OE′交点的一个双数(0或2或4等);假如我们由OG和OE′的任何一个交点沿OG到其他交点,我们也必须经过OG和OE交点的一个双数。自然,单独的几何证明也可得到这个结论。
其次,让我们假定,A是OE和OG曲线上的一个稳定均衡点;F是情况变化后交换指数向之移动的OE′和OG曲线上的一个稳定均衡点。让我们研究一下,F可能在什么位置。画直线如第二十七图。这就是,让水平线TA′AR通过A割Oy于T及OE′于A′。画垂直线HASV切Ox于H,并将直线OA′延长于V;画垂直线H′UA′V′割Ox于H′,并割直线OA于U.〔在图中没有指出F,因为它在图中各部分的运动还在研究中;如不分别画出各种可能的综合情况,就不能指出它的位置。〕

这样我们就得到以下结果:假如OG属于正常类型,F必然是位于OAT三角形之内;假如属于第一类型,F必然位于yOAV范围之内;假如属于第二类型,就这个条件来说,F可位于HV左边的任何地方。
同样,假如OE′属于正常类型,F必然位于OA′H′、V′A′SV范围内的某一地方;假如属于第一类型,F必然位于OBHAA′、yTA′SV范围内;假如属于第二类型,就这条件来说,F可位于HV左边的任何地方。综合这些条件,我们得:
首先,假设OG属于正常类型:
(1)令OE′属于正常类型,则F必然位于OA′H′三角形之内,例如a;
(2)令OE′属于第一类型,则F可能位于OAA′三角形之内的任何地方,例如a或b;
(3)令OE′属于第二类型,则F可能位于OAT三角形之内的任何地方,例如a、b或c.
其次,假设OG属于第一类型:
(1)令OE′属于正常类型,则F可能位于OA′H′、V′A′SV范围内的任何地方,例如a或d;
(2)令OE′属于第一类型,则F可能位于OA′A,yTA′SV范围内的任何地方,例如a、b、d或e;
(3)令OE′属于第二类型,则F可能位于yOAV范围内的任何地方,例如a、b、c、d、e或f.
第三,假设OG属于第二类型:
(1)令OE属于正常类型,则F可能位于OA′H′、V′A′SV范围内的任何地方,例如a、d或g;
(2)令OE属于第一类型,则F可能位于OHAA′、yTA′SV范围内的任何地方,例如a、b、d、e、g或h;
(3)令OE属于第二类型,则F可能位于HV左边的任何地方,例如a、b、c、d、e、f、g或h.
这些结果不能用一个简短的定理来总结,但可用如下方法来表示:
OE′正常类型位于<OA′H′之内
OG正常类型位于<OAT之内
OE′第一类型位于OA′A之内
OG第一类型位于OAS之内
OE′第二类型位于OH′A或OA′T之内
OG第二类型位于OAS或OAH之内。
如OG所属类型为----正常----——----——----Ⅰ----——----——----Ⅱ——----——
而OE所属类型为----正常----Ⅰ----Ⅱ----正常----Ⅰ----Ⅱ----正常----Ⅰ----Ⅱ
则F可能移动到的点为a----a或b----a、b或c----a或b----a、b、d或e----a、b、c、d、e或f----a、d或g----a、b、d、e、g或h----a、b、c、d、e、f、g或h
在每种情况下,E输出的棉布数量都减少。在G曲线属于正常类型或第一类型的每种情况下,交换比率都对E有利。在G曲线属于正常类型的每种情况下,麻布量都减少。只有在E曲线属于第二类型时,才能达到c和f的位置;只有在G曲线属于第二类型时,才能达到g和h的位置。
|