首页 -> 2005年第11期
促进课堂动态生成的“四要素”
作者:林传忠
预设——课堂生成的“奠基石”
案例:(教学内容:“正比例关系的认识”)
师:同学们,你们有没有做过绕口令的游戏?有这样一个绕口令,第一句是:一只青蛙,一张嘴,两只眼睛,4条腿,谁能来接下面一句。
生1:两只青蛙,两张嘴,4只眼睛,8条腿。
生2:3只青蛙,3张嘴,3只眼睛,12条腿。
生众笑:错了,错了
师:为什么错了?
生众:应该是6只眼睛。
师:对,如果让同学们再说下去,能说得完吗?
生:不能
师:现在老师告诉你青蛙的腿有36条,你能猜出青蛙有几只吗?
生略加思考:9只青蛙
师:你是怎样得出9只呢?
生:36÷4=9
师:为什么要除以4?
生:因为每一只青蛙都有4条腿,这个数是不变的,所以要除以4。
师:说得好,现在同学们就把这个表填好。

(生填完。)
师:你们发现了什么?
(生思考后。)
生1:青蛙的腿数总是青蛙只数的4倍。
生2:青蛙只数变了,青蛙的腿数也变了。
生3:我补充一点,青蛙的只数变多,青蛙的腿数也变多,青蛙的只数变少,腿数也随着变少。
师:同学们观察很认真,善于发现规律,真了不起!现在哪位同学能把刚才说的总结一下?
生:青蛙的只数变多,青蛙的腿数也变多,青蛙的腿数都是青蛙只数的4倍。
师:说得好!你已把我们今天要学的知识说出来了,这就是我们今天要研究的“正比例关系”。(教师板书:正比例关系)现在我们就来进一步来研究正比例。
教学预设是教师在教学活动之前,根据教学目标和要求运用恰当的教学方法,对教学活动诸因素进行分析和策划的过程。它是上好课的前提和保证。关注课堂教学的生成性并不是不要预设,恰恰相反,课堂的生成机制的高效发挥正是依赖于教师精心的预设。那种认为不认真备课也能有课堂生成的想法是极其错误的。预设是生成的“奠基石”,而生成则是对预设的超越。本案例中正是由于教师精心预设了一个绕口令的情境,触动了学生已有的经验,才激起了学生的学习欲望,在教师有效的引导下,学生才生成出了要学习的内容。
对话——课堂生成的“催化剂”
案例:(教学内容:“分数能化成有限小数条件的判定”
……
师:老师有一种特异功能,就是不用计算就能很快地判断出一个分数能否化成有限小数。不信,同学们就写一些分数让老师来展示一下特异功能吧。
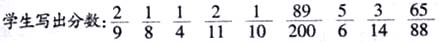
教师判断,经学生用计算器检验,表明教师的判断都是正确的。
生:老师,你肯定有一种方法,要不然没有这么快判断的。
师:对!同学们也想有这样的特异功能吗?现在请同学们把刚才的分数,按能化成有限小数的归为一类,不能化成有限小数的归为一类,再仔细认真地观察,看看能有什么发现?
(学生经过思考。)
生1:我觉得可能与分母有关,因为我们把分数化成有限小数都是把分子除以分母。
生2:对,我仔细地算了2/9化成小数的过程,除不尽,是循环小数,如果分母换成5就可以化成有限小数,所以我也觉得与分母有关。
生3(兴奋地)说:我发现了分母是2或5倍数的分数才能化成有限小数。
生4:我补充一下,应该是把分母分解质因数后,分母只含有2或5的分数才能化成有限小数。
师:不错,说得有一定的道理,但是不是真的是这样,同学们现在就利用这个结论进行一下验证。
生众进行验证后,都认为这个结论是对的。
师:老师这里也有一个分数3/15,同学先判断一下它能不能化成有限小数?
生5:不能化成有限小数,因为分母中含有约数3。
生众:对,不能化成有限小数。
师:还有没有不同的意见?
生6:这个分数能化成有限小数,是等于0.2。
师:是呀,这是怎么回事?
(生众都在纳闷。)
有一位学生欲言又止,师用亲切的目光鼓励,“你说,没有关系。”
生7:我发现前面我们判断时,分数都是最简分数,而3/15不是最简分数,可能是这个原因吧。
生8:有道理,如果把3/15化成最简分数就是1/5,当然就能化成有限小数了。
师:那如何去判断一个分数能不能化成有限小数呢?
生9:分母只含有2或5两个质因数的分数,才能化成有限小数,但这个分数必须是最简分数。
……
新课程理念下数学课堂教学已不是把学生当成容器进行灌输式的传授,而是师生、生生平等对话、沟通交流的学习过程。在案例里,学生在对话中相互质疑、相互补充,不断“催化”生成新的知识:先是认识到“一个分数能不能化成有限小数与它的分母有关”,进而发现“能化成有限小数的分数的分母质因数只能含有2或5”,最后得出完整结论:“一个最简分数,分母只含有2或5两个质因数的分数,才能化成有限小数。”在对话中,学生的见解和生活经验不断完善、提升;在对话中,教师准确把握了学生已有的知识经验,进行了富有针对性的引导。当教师发现学生得出“能化成有限小数的分数分母质因数只能含有2或5”这个不完善的结论时,提出“3/15”这个分数,再让学生进行对话,把对话不断引向深入,最后学生在对话的“催化”下,得出能化成有限小数的分数的特征来。可见对话是课堂生成的“催化剂”。
等待——课堂生成的“酝酿坛”
案例:(教学内容:“分数基本性质”教学后,一道判断题)
教师出示判断题:
如果1/a=7/b(a、b都不为0),那么b是a的7倍……………………………( )
(学生独立思考2分钟,教师巡视并进行个别辅导,2分钟过去了,只有几位学生举手。)
师:能说说理由吗?
生又进入思考之中。
过了一会儿,很多学生已举起了手。
师(示意一位学生):你说说看。
生1:这道题是对的,如果a等于1,要使1/a=7/b,那么b就要等于7,所以b是a的7倍。
生2:我是这样想的,分数1/a的分子1到7,扩大7倍,所以分母也要扩大7倍,1/a=7/7a所以7a=b了,b就是a的7倍了。
生3:我的想法与生2有点相似,但我是想7/b的分子7到1,是缩小了7倍,要使这两个分数相等,根据分数的基本性质,分母也要缩小7倍,b缩小7倍正好是a,那b没有缩小时就是a的7倍了。
……
等待是一种耐心,更是一种艺术。在本案例中,教师留给出一定的时间给学生思考,教师耐心等待,但学生无法得出结果,教师又给出时间让学生再进行思考,教师还在等待,最后在足够的时间里,学生“酝酿”生成了自己富有个性的理解。因此,教师要能等待,要善于等待,教师布置思考任务给学生时,就要给出时间让学生进行真正意义上的独立思考,进行酝酿,让他们在已有的旧知找到新的生长点,把所学的知识融入到自己的知识结构中,课堂的生成自然就产生了。如果没有教师的等待,没有学生的酝酿,课堂的生成就无从谈起。
宽容——课堂生成的“保护伞”
案例:(教学内容:平行四边形面积计算)
(让学生拿出已准备好的平行四边形、小剪刀、尺子和其他工具)
师:现在同学们就利用准备好的工具和已学过的知识,想办法求出手中平行四边形的面积。
(生动手实践,教师巡视,一段时间后,大部分学生已举手,教师让学生汇报。)
生1:我是用平行四边形的两条边相乘得出面积的。
生众:错了,错了。
师:让生1把话说完。(对生1说)你是怎样想的?
生1:我是由长方形的面积等于长乘宽类比推理过来的。
师:那是不是可以这样类比推理呢?
生1(想了一会儿,不好意思地):我也说不清楚。
生2:生1的做法是错的,应该是把平行四边形剪拼成长方形,因为长方形的面积我们已经会算了,所以平行四边形面积也就能求出来了。
(教师让生2同学展示剪拼过程,使全班学生看到平行四边形的面积是等于底与高的乘积,而不是两条边的乘积,生1也知道了错误,明白了其中的道理。)
师:好,刚才生1虽然做错了,但我们要感谢他,因为他给我们带来一种方法类比,类比是发现新事物一种很重要的方法,许多发明创造都是由类比得出的。(师生共同鼓掌,生1脸上写满了自信与喜悦)生2运用了转化的思想,把新问题转化成已学的知识,进而解决它,这是非常重要的思想,希望大家能学会这种思想。
……
课堂随机生成的内容是学生真实水平的反映,正因为真实,错误就自然难以避免。对学生随机生成的错误知识、观点、看法,如果教师一棒子打死,那失去的将是一个敢于思考的生命,课堂的生成也就被“打死”了。这个案例中老师的高明之处,就在于对这位学生生成性的错误的宽容,并从其错误中挖掘出可借鉴的知识,不仅让全班学生从中受益,更让这位学生在错误中找到自信,赢得在同学心目中的地位。可见宽容是课堂生成的“保护伞”,在教学中,教师要对学生生成的错误予以宽容,让学生在宽容的“保护”下,大胆展示,真情告白,个性张扬,这样课堂的动态生成也就呼之欲出了。