首页 -> 2006年第4期
“四点”架起分数应用题
作者:马甫波
一、意义为本
意义的含意极其丰富,因而也极其抽象,与学生的已有知识存在相当距离,因而教师在教学时,会忽略意义教学,重视数量关系教学,忽略了意义到数量关系的连接,造成意义与数量关系的因果断层。“根深”才能“叶茂”,有了对意义的深切体会理解,才能更好地领悟数量关系,所以要重视意义教学,以意义为基石,为学生提供丰富的思想源泉。
1.感知意义
对分数应用题解答起关键作用的有三个意义:分数的意义、百分数的意义、一个数乘以分数的意义。理解了分数、百分数的意义就能区别是数量还是分率(关系),理解了一个数乘以分数的意义,就抓住了三类应用题的核心所在,为学生进一步探究指明了方向,教学时可从以下三个环节入手。
(1)从存在中感知意义
感觉到意义就在身边,就会使学生觉得意义不是那么遥不可及,可增加亲近感。如教学一个数乘以分数的意义时,可从一个数的几倍是多少出发,接着利用迁移,观察得出一个数乘以分数的意义。这样使学生感知一个数乘以分数的意义与一个数乘以倍数的意义的联系,淡化意义的高不可攀的形象,从而达到可接受性,达到可理解性。
(2)从有用中感知意义
感觉到了意义有用,就会想到使用它,从而会更好地感知意义。如看式画图:9×4/5,因为它表示9的4/5是多少,把9看作单位“1”的量,平均分成5份,求4份是多少,以此指导画出图(见下图),这样树立起意义为本、意义可用的理念,从而激发起使用意义的动机。
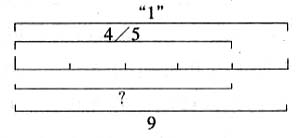
2.提炼意义
意义是基层的,列式解题等各意识形态都是从其基础上产生的,让学生从意义出发进行提炼,更有助于学生内省、领悟,激发出思维的火花。
(1)意义与解题策略
在学习了百分数的意义后,就抓住百分数是表示一个数是另一个数的百分之几这点出发,凡见到题目中有一个百分数的,就要求学生说出谁是谁的百分之几。这样一来一举四得:一是直接地加深了百分数意义的理解。二是突出了百分数
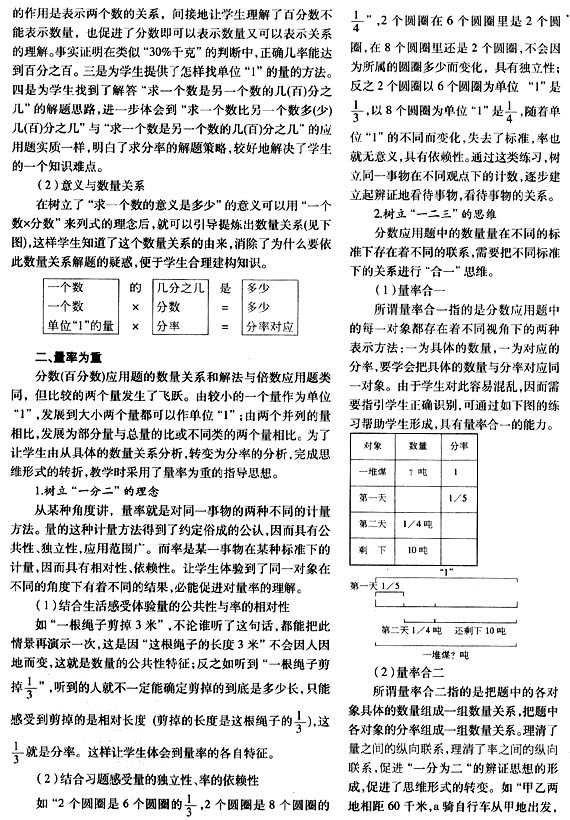

其次创设画图机会,强化用图,教学时,可先出示图,然后编题,图文结合理清思路。巩固时,每一习题都要先画图,加强练习,让学生掌握画图技巧,养成画图的习惯。
四、正逆一体
小学数学的核心内容之一就是正向思维与逆向思维的统一。分数应用题把这一思想表现得淋漓尽致,教材安排由乘到除,由一步到两步,客观上强调了分类教学,采取“单线”的教学,在综合时,易造成学生的思路混乱,因而主张正逆一体,强化正逆思路的融合,形成思路。
1.以正带逆、逆中见正
当正向思维的应用题为学生所接受时,适当改变条件转化为逆向思维的题目,创设认知冲突,激发学生自省、建构。如教学“求一个数的几分之几是多少?”的应用题,学生经历读题、画图、分析、列式等过程,体验到数量结构,然后改变信息,变成“已知一个数的几分之几是多少,求这个数”的应用题,鼓励小组合作,探究可以怎么解决问题。从题目、从图、从数量关系、从方法等感受由正到逆,逆中有正的联系,得出解决方法。以求正逆同步前进,同步温故。
2.正逆对比、形成思路
为了让学生形成思路,重点进行了审题训练,弄清是谁与谁比,判断被比的量是单位“1”的量,则与它比的量是分率对应量。明确了哪个量是单位“1”的量,如它是已知量,求它的几分之几是多少,宜用乘法解,如它是未知量,已知一个量的几分之几,求单位“1”的具体数量,宜用除法解。这是分析分数应用题的思维过程,也是解题的要领。通过正逆对比以形成思路。如可通过找关键句对比、通过图式对比,类型对比等方式,逐步体验得出找单位“1”的量的方法,这样在对比练习中,无论应用题的条件如何变化,学生都能抓住应用题的数量关系,找到解决问题的途径和方法。
责任编辑:李海燕