首页 -> 2006年第6期
《三角形内角和》教学设计
作者:汪明峰
苏教版教材第七册第130~131页例1、例2,“练一练”和练习二十五。
教学目标:
1.使学生理解和掌握三角形内角和的结论,并能应用这一规律解决一些实际问题。
2.通过测量、动手操作和小组合作等实践活动,培养学生观察、抽象、概括的能力和创新意识。
3.发展学生的逻辑推理能力。
教学过程:
一、激趣导入
1.做七巧板拼图游戏。(渗透数学思想方法)
2.出示一组三角形(如下图)。

(1)教师指出:三角形的每一个角叫做它的内角。(板书:内角)
(2)提问:现在要想知道三个内角分别是多少度,怎么办?
学生动手量一量(手中的三角形),然后汇报测量结果。
3.游戏:由学生报出手中三角形的任意两个角的度数,老师迅速说出它的第三个角的度数。
(可多点几名学生出题,教师要很快说出结果,学生肯定为之惊奇。)
谈话:同学们想不想知道老师的秘诀!
其实只要留心观察,三角形三个内角度数之和是有一定的规律的。今天我们就一起来探索这个规律。(把课题板书完整)
设想:通过复习已学过的知识,将学生引进学习新知识的最近发展区,找准新旧知识的连接点。通过七巧板游戏,向学生渗透转、移、拼等数学思想方法,为下面验证规律埋下伏笔。游戏设计激发学生的好奇心和求知欲,学生对老师的神速反应和准确作答感到惊奇,产生了强烈地解开“谜团”的欲望,为学习新知作了充分的准备。
二、实践探究,初步感知
1.谈话:三角形三个内角之和之间究竟有一个什么样的规律呢?请同学们就以上面的三角形为例动手算算看。
2.学生算后,指多名学生回答,问:根据你的计算你认为三角形三个内角之和应存在着什么样的规律?
(三角形的三个内角之和是180°。如果学生的答案不是准确的180°,师小结时只要提一个“模糊概念”,以进一步激发学生探究的欲望。)
设想:让学生自己动手“算一算”并大胆归纳,主动探索,初步感知规律,培养学生通过实践发现并获得知识的能力。
三、实验验证,得出结论
l.谈话:光用量角器,还不能完全证明这一规律是不是具有普遍性,我们可以用实验的方法,来验证发现的这一“规律”是否正确。那么如何验证呢?
2.让学生分组讨论、研究验证方法。教师巡视指导,鼓励学生用不同的方法去验证。
3.小组汇报实验方法及结果并演示。(可能会有以下几种情况)
A组:用折叠法,将三角形的三个内角向形内折叠,使三个内角的顶点交于一点,三个内角边两两重合。得出一个平角,也就是三个内角之和等于180°;
B组:用割补法,先割下三角形的三个内角,再把这三个内角拼到一起得出了三角形内角和是180°的结论;
C组:用一个平角去比较的方法,先在纸上画一个平角,再将三角形一个内角的一边与平角的一边重合,顶点与顶点重合,沿这个角的一边画线,用这样的方法依次画完另两个角,而得出内角和是180°结论。
在学生说明验证方法的同时上台演示(多媒体课件配合学生演示),然后指名学生评价。最后让学生把自己喜欢的方法,再次介绍给同桌听。
4.得出结论。
谈话:同学们真爱动脑筋,想出了这么多解决问题的办法,根据上面我们的实验可以得出三角形的内角之和是180°。(板书结论)
5.指导学生进一步阅读课本第130页。
6.小结方法及结论。
同学们真了不起,我们通过量一量、算一算,就初步发现了规律,并通过折一折、拼一拼、比一比、议一议等方法实验验证了三角形内角和是180°这一规律。“观察——猜想——验证”这是一种有效的数学学习方法,希望同学们在今后的求知过程中能经常运用。
设想:学生是课堂教学的主体,把课堂的发言权让给学生,并引导学生主动探索解决问题的办法。通过不同途径去验证设想,不仅让学生亲历知识产生的过程,对新知识产生深刻的印象,又培养了学生自主学习的能力;既让学生体验到成功的快乐,又激发了学生的创新欲望。
四、实际应用,内化新知
1.(出示)例1三角形中,己知∠1=75°,∠2=34°,求∠3的度数。
读题后,指名学生说一说是除了∠1,∠2两个已知条件外,你还能想到什么已知条件?∠3如何求出来?然后学生独立完成例l。
2.“练一练”。
学生独立完成,并说说∠2是如何求出来的?
3.(出示)例2一个等腰三角形的顶角是90°,每个底角是多少度?(如图)
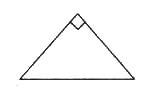
指名说一说,等腰三角形两底角有什么关系?然后指名板演,集体订正。
思考:等边三角形,三个角的度数分别是多少呢? (先让学生想想等边三角形三个内角的关系,再解答)
4.练习二十五的第l题。
学生先分组练习,再通过实际测量检验计算结果。
5.学生独立完成练习二十五的第6题。
设想:在学生已掌握规律的基础上,通过实用练习,既能巩固新知,又能形成能力。
五、质疑问难,深化提高
1.媒体演示:王小明要想在钉子板上围一个包含有两个大于或等于90°角的三角形,可怎么也围不出来,急得满头大汗。为什么?你能帮他解答吗?这个例子能说明什么?
2.我家的邻居电工张师傅遇到这样一个难题:由于开挖下水道,一根电线杆的斜拉索需移动位置,使得拉索与电线杆的夹角为60°。你能运用我们所学的知识,帮助张师傅轻松解决这一难题吗?
3.一个三角形的一角是50°,则另两个角的度数可能是多少度?
积极鼓励学生提出不同的见解。
设想:数学知识源于生活,又用于生活,通过具体实例,使学生体验到数学知识在现实生活中的作用,这一环节的设计旨在训练学生能用新学的知识解决实际问题的能力。同时通过练习培养学生的创新意识,加深数学与实际生活的联系。从而激发学生学好数学的热情。
六、全课总结
学了今天这节课你有什么收获?这些收获你是怎么得到的?
设想:这样的结束语,学生既可以讲课本学到的知识,也可以讲学习知识运用的数学思想方法。通过学生的回答,不仅可以反馈学生本节课的学习情况,同时也充分体现学生的主动性和主体性。
七、课外作业
思考:如果把一个三角形放在放大镜下面,那么这个三角形内角和会变化吗?
责任编辑:李海燕