首页 -> 2006年第11期
谈数学品格的培养
作者:杨峰梅
一、 在形式多样的思维活动中培养积极的思维态度
数学学科积极的思维态度表现在:从来不满足于观察、直观,而总是通过积极的比较、抽象去揭示事物的本质,即不断抽象化;从来不满足于特例,而总是通过归纳和概括一系列特例的共同的、本质的特征,进而反映一类事物的一般性质或规律,即不断一般化;从来不满足于局部范围内的统一,总是抓住否定局部范围统一的奇异现象,去揭示更大范围的统一,即不断统一化。
在教学中,我注重精心设计、选择数学材料,引领学生进行抽象、概括等思维活动,在抽象化、一般化、统一化等过程中,升华数学思维,培养积极的思维态度。
案例1 小名带了20元钱去商场买文具,下面是小名与营业员的对话——
小名:“阿姨,我想买5本笔记本。”
营业员:“好的,笔记本的单价有三种:4.5元,3.2元,2.8元,你准备买哪一种?”
小名:“我买单价是3.2元的。”
营业员:“剩下的钱怎么办?”
小名:“全部买圆珠笔吧。”
营业员:“正好够买2枝。”
请你根据两人的对话,列式计算出圆珠笔每枝多少元。
面对具体复杂的情境,让学生说说这段话表达了什么意思。学生积极思维,抽象出:小名带了20元钱,买5本笔记本,每本3.2元,剩下的买2枝圆珠笔,每枝圆珠笔多少元?经过抽象化后,学生把握了本质,正确地列式解答:(20-3.2×5)÷2=2(元)
案例2 任选两个不相同的数字(0除外),用它们可组成两个不同的两位数,用其中的大数减去小数,再重新选择两个不相同的数字,重复上述过程,像这样连续操作4次。
()-()=()()-()=()
()-()=()()-()=()
从上述过程中,你发现了什么?
学生兴致勃勃地操作、观察,从这些特殊的例子中,概括出了这一类情况的规律:所得的差是9的倍数。所选两个数字的差是几,式中所得的差就是9的几倍。
案例3 有一堆糖果,如果3块3块地数,最后余2块;如果5块5块地数,最后余4块;如果7块7块地数,最后余6块;这堆糖果最少有多少块?
粗读此题,三种数的情况有相同点,即每次数后均有余数,但余数不相同。孩子们积极动脑,用转化的思想方法,使三种数法统一为,不管哪种数法都少一块。这样,如果添上一块糖,用三种数法数都没有余数,即糖的块数至少为3、5、7的最小公倍数105,减去添上的一块,求得这堆糖最少有105-1=104(块)。在统一化的思维过程中,在探索、交流中,孩子们态度积极,思维活跃。
二、 在具体可感的情境操作中寻求科学的思维方式
科学的思维方式一方面指通过秩序、和谐、对称、整齐、简约等形式来表现与之联系的思维情趣,并在此基础上,形成学习或研究科学以及从事创造性劳动的具体方法。另一方面指注重定量分析,注重形式逻辑,注重抽象思维。
在数学课堂中,我注重有意识地引导学生借助于直观手段,去探索、寻求科学的思维方式,巧妙地解决问题。
案例4 快车和慢车同时从东西两站相对开出,第一次在中点西侧10千米处相遇,相遇后两车以原速前进,到达对方出发地后,两车立即返回,在途中第二次相遇,这时相遇点距东站40千米。东西两站相距多少千米?
出示题目后,用CAI课件进行演示,再让学生试着画出线段示意图,去寻求解决策略。生1:快车和慢车合走一个全程,快车即比慢车多行10×2=20(千米),现在它们共合走了三个全程,即快车比慢车共多行20×3=60(千米),从示意图中可以看出当快车和慢车合走完两个全程时,它们各自正好走了一个全程。由此可知,在合走第三个全程时快车比慢车多行60千米,即在第三个全程中,慢车走了40千米,快车走了40+60=100(千米),一个全程为40+100=140(千米)。生2:设全程的一半为X千米,因为快车和慢车合走一个全程时,慢车行了(X-10)千米,那么与快车合走三个全程行了(X-10)×3千米,从示意图中可以看出慢车共行了一个全程再加40千米,由此可列出方程(X-10)×3-40=2X,解得X=70,东西两站相距70×2=140(千米)。看似无从下手的“难题”,找到科学的思维方式,问题就迎刃而解。
三、 在实际需求与矛盾冲突中诱发强烈的思维内驱力
在数学自身的发展中,在数学内部发展与外部需要相适应的过程中,在数学材料与人的认识的相互关系中,都存在着大量的矛盾,揭示、分析、解决这些矛盾的需求便产生了所谓的思维内驱力。
在教学中,我经常设计一些生活数学题,如数学材料与学生的认识产生矛盾冲突的习题,以此来诱发学生的思维内驱力。
案例5 为创建全国卫生城市,保证学生的卫生安全,学校决定给每个参加日托的学生配一条毛巾。“五山”牌提花毛巾的统一标价是每条6元,在近期促销活动中,超越超市打八五折,如海超市“买五送一”。学校要买630条毛巾,到哪家购买较合算?
社会生活的需要,使孩子们产生思维内驱力,去寻求适应需求的数学相关知识点并合情推理。生1:6×85%=5.1(元), 6×5÷(5+1)=5(元),所以去如海超市购买较合算。生2:6×85%×630=3213(元),630÷6×5×6=3150(元)所以去如海超市购买较合算。
案例6 甲乙两列火车同时从AB两站相向开出,在离A站70千米的地方相遇后,两车仍以原速度继续前进,各车分别到达对方出发点后立即返回,又在离B站20千米的地方相遇,AB两站相距多少千米?
要求“AB两站相距多少千米?”要是知道两车的速度、所行的时间就好了,可是题目中没有常规分析所需要的条件,数学材料与学生的认识产生了矛盾冲突。怎样才能解决这个问题,学生的思维内驱力应运而生,解题策略也随之而来:第一次相遇时,甲乙两列火车所行的路程之和,正好是两站相距的路程,也就是说,当甲乙两列火车合行完AB两站间的全部路程时,甲火车行了70千米。第二次相遇时,甲乙两列火车合行的路程是两站间距离的3倍,因此,这时甲火车所行的路程是70×3=210(千米)。但甲火车实际行的路程是AB两站间的距离加返回的20千米,所以AB两站间的距离为210-20=190(千米)。
四、 在感性操作与理性思辨中提高密集的脑力当量
数学学习的脑力付出在学生的脑力总付出中,具有突出的地位,数学无疑是发展人的脑力的最为重要的学科。
在教学中适当设计一些趣味题,带领孩子们去感悟,去思辨,发展脑力,提高脑力当量。
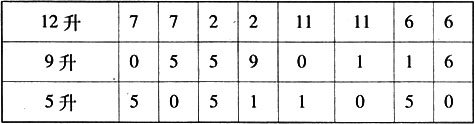
案例7 一只桶里装着12升菜油,要把这些油平均分成两份,但没有称量工具,只有能装9升和5升的空桶,你能办到吗?
根据题中的已知条件,准备教具,先让学生感性地倒一倒,由于仅仅依据感性认识活动——无理性地倒来倒去的话,很难得出所需结果。因而,直接提取材料,引导学生进行适当的数学组织化和逻辑组织化,即付出更多的脑力代价,才有可能寻找出通向解决问题的最佳途径。(如下表所示)
 |
|