首页 -> 2007年第1期
突破数学教学难点的四大策略
作者:傅建霞
一、 瞻前顾后,提前渗透
数学知识之间存在着紧密的联系,有些知识技能的掌握对后面的学习起着至关重要的作用。如果前面的教学中忽略了这些知识技能的训练,后面的学习就会出现问题。如计算39×8时,需要24+7的口算技能。但教材在安排两位数加一位数的口算时,考虑到学生的知识基础而未出现与乘积有关的两位数加一位数的口算如3×8+7等。这样学生在学习两位数乘一位数时,虽然已有两位数加一位数的口算基础,但后面需要的却是与乘积有关的两位数加一位数的口算技能,因而在计算两位数乘一位数时,错误率最高的就是乘加这一环节,因为这时看不到两个加数,只能边想边算。
要突破这类教学难点,光凭课上的专项训练或临时突击训练只能是杯水车薪,因为技能的形成需要一个过程。因此不管我们使用的是哪一种教材,都必须确立“用教材教”的理念,在备一节课时,不能只看到教材上呈现的内容,还要把每一节课放在整体学科教学的系统中加以通盘考虑,努力做到瞻前顾后,要在弄清所学知识是今后学习什么知识的基础后,还要根据学生现有的基础和今后学习的需要进行可能的合理的拓展训练,为后继学习做好知识和能力的准备。如教学两位数加一位数的口算时,如果知道这是两位数加两位数口算的基础,而且还是今后学习乘法计算的基础,教学时,就会加强与乘积有关的两位数加一位数的口算训练,但是学生还未学习乘加的混合运算,因而可以改为进行连着算的听算练习,如教师说三乘八再加七,要求学生先乘再加后写出最后的结果。
这样既可以避免乘加的运算顺序问题,提高两位数加一位数的口算能力;又训练了学生与乘积有关的两位数加一位数的听算技能,为突破两位数乘一位数的教学难点提供有力的保障。
二、 再现生活,由景触思
由于数学具有高度的抽象性,这就使学生在理解时常常是勉强知其然,很难知其所以然,运用时只能依葫芦画瓢,稍有变化就会出错。要突破这类教学难点,苏霍姆林斯基曾给我们提过一个建议,就是当学生不能解决某个问题时,只要带他到实地去看一看,那什么问题都会迎刃而解。虽然课上四十分钟的时间我们不可能带学生到实地去,但我们可以利用多种教学手段,给学生创设一个真实的情境,利用生活情景激活学生已有的生活经验,触发学生的思维灵感,通过情景、经验、思维的交融使学生产生顿悟,从而深刻理解抽象的数学知识。
如教学《分数的基本性质》时,我们创设了这样一个情境:(教师讲述的同时多媒体演示分的过程及结果)一天,小明带着三个同学回家做作业,妈妈拿出一个大饼招待大家。开始妈妈将饼平均分成4份,每人拿一块,可小明说他想吃两块。于是妈妈重新将这个饼平均分成8份,每人拿两块,可小明还嫌少,他说要吃三块,妈妈有些生气。于是第三次就将饼平均分成16份,让小明吃了三块,小明高兴地吃起来,吃着吃着,发现有些不对劲,好像三块还没有原来的一块多,这是怎么一回事呢,你们能给他说说其中的道理吗?
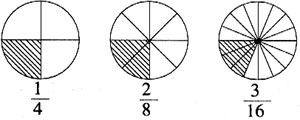
由于创设了真实的生活情境,学生的生活经验被激活,再加上数和形的有机结合,学生很快说出了其中的道理:将一块饼平均分的份数扩大4倍,每份的大小会比原来缩小4倍,要想使积不变,取的份数必须跟着扩大4倍,现在取的份数只扩大了3倍,所以结果变小了。这样学生就从本质上理解了分数的基本性质。不管数学有多么抽象,它始终来自于现实世界,只是对现实世界进行了科学的抽象而已。只要我们善于联系生活,就会从中发现与数学知识相连的情境、情景等,从而找到突破难点的钥匙。
三、 巧打比方,借事说理
因为数学来源于生活,它是对现实世界的抽象概括。因此根据世间万物都是有联系的观点,在突破某些教学难点时,我们可以采用打比方的方法,借助学生在生活中经历过的、印象较深的事情,以简单明白的事理来说明抽象的数理,通过两者之间的共通性促进学生对数学知识的理解和掌握。
如学生学习减法的性质“从一个数里连续减去两个数,等于从这个数里连续减去这两个数的和”时,在观察、比较并得出这一结论后,我打了一个比方:从一个数里连续减去两个数,就好比老师现在要将脚上的两只鞋扔到教室外面,我可以用两种不同的方法:一种是一只一只地扔,第二种是先将两只鞋捆扎在一起然后一下子扔了,结果都一样,都是将两只鞋扔到了外面。通过这一比方,学生不仅明白了这样算的道理,在改变运算顺序时,运算符号和括号的使用,错误很少;而且在学习除法的同一性质时,我未开口,学生就能变换自如,有个学生当时还对我说:这简单,你不是说过扔鞋子的事吗?可见,小比方有时可以帮大忙,既可以突破教学难点,又使数学教学变得生动有趣。虽然数学具有高度的抽象性,但对于刚刚开始学习数学的小学生来说,严格的不理解还不如不严格的理解,因为只有真正理解了的知识,学生才能掌握和运用。
四、 构建数模,架桥飞跃
小学生思维是以具体形象思维为主要形式,他们在学习一些抽象的数量关系时,常常是借助直观能够理解和运用,一旦离开直观就无从下手,不是根据例题猜算法就是根据个别词语定算法,如见多就加见少就减等。由于课堂教学的时间有限,再加上培养小学生初步的逻辑思维能力是数学教学的目标之一,因此我们不可能也不能一直让学生借助直观解题。要突破这类教学难点,教学时要注意充分利用简单的半抽象的直观图、式等,帮助学生在头脑中建立数学模型,架好具体形象思维和抽象逻辑思维之间的桥梁。
如求比一个数多几的数的应用题,教学例题时,教师一边引导学生分析:哪个多,哪个少?多的可以分成哪两部分?一边帮助学生建模,即根据学生的回答相应地画出长条图:

学生由于有了操作的基础,这时借助半抽象的长条图就能很快找到例题的算法并明白这样算的道理。完成后面的“想想做做”时,在学生分析哪个多、哪个少,多的可以分成哪两部分时,教师仍然相应地指上面的长条图。这样通过多次的说和指,就使比较数量多少的过程与长条图有机结合起来,也使黑板上的长条图变成学生头脑中这类应用题数量关系的模型。当离开直观图解题时,随着两个数量多和少的比较,学生头脑中就会出现长条图,从而顺利地找到解题思路。当学生有了一定的解题经验后,再引导他们将例题和“想想做做”等题进行比较,说一说为什么都用加法算?借助数模和已有的解题经验,学生就能很快发现并理解“较大的数总可以分成两部分,要求较大的数,就要将两部分合起来,用加法算”这一规律,从而顺利过渡到运用这一规律解题。因为小学生抽象逻辑思维仍然具有很大成分的具体形象性,我们只有想办法使学生头脑中有图或式,他们才能逐步摆脱具体形象的束缚,顺利地向抽象思维过渡。
突破教学难点的策略还有很多,以上仅是我们在教学实践中的一些行之有效的做法,仅供大家参考。但不管我们选择哪一种策略,都必须本着以学生为本、以学生的发展为本的理念,遵循有效性原则,这样我们的课堂教学才会环环精彩,堂堂高效。
责任编辑:李海燕