首页 -> 2007年第4期
警惕数学思维过程中的“隐性牵引”
作者：王志南
教学片断：教学苏教版P44例1
师：我们共同回忆一下分数乘法应用题依据的数量关系式。
生：单位“1”的量×比较量对应的分率=比较量
师：对，首先请同学们用这个数量关系式来解答复习题。
学生解题，汇报。
师：接下来请同学们自主阅读例1，分析题中含有怎样的数量关系式。
出示苏教版P44例1
西林果园有桃树360棵，占果树总棵树的
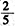。西林果园有果树多少棵？
师：这道题中单位“1”的量是什么？比较量是什么？谁又是比较量对应的分率？
生：把果树的总棵树看作单位“1”的量，比较量是桃树的棵数，
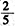是比较量对应的分率。
师：回答得很好！那么谁能找出这道题中含有怎样的数量关系？
生：果树的总棵数×
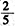=桃树的棵数
师：果树的总棵数是已知的还是未知的？(生：未知的)对了，我们可以用上面的数量关系列方程解答。
引导学生解设，列方程解答。
师：如果用算术方法解答，你会吗？(生：会)
师：让我们一起来看数量关系，这道题已知什么量和什么？要求什么？
生：已知比较量和比较量对应的分率，要求单位“1”的量
师：(板书：单位“1”的量×比较量对应的分率=比较量)根据乘法各部分之间的关系，单位“1”的量该怎么求？
生：比较量÷比较量对应的分率=单位“1”的量
师：好，下面请同学们独立用除法来解答这道应用题。
和这位老师课后交流的时候，他感慨地说，这班孩子，平时倒挺活跃的，听课老师来了，有些紧张，不敢回答主动问题了。在给这位老师定教学评定等级的时候，按理说，对这样一堂教师分析教学内容到位，教学层次清晰，引导学生思考有序，学生配合融洽的课，给个A级是适合的。(共A､B､C､D四级，A为最高级别)然而，反复回味这堂课，总觉得这教学过程缺少了些什么？总让人感觉心里有点疙疙瘩瘩。
思考这个问题到了晚上，才觉眼前一亮。在帮助学生理解例1题意的时候，教师一步一步引导学生分析题意，示意学生用列方程解答。在教学用除法解答例1的时候，学生已有的基础，已完全有能力用除法来解决例1，然而教师还是不放心，继续提问学生思考如何用除法解决问题？这样的牵引不仅多余，而且掠夺了学生的自主思考权。
仔细回味这一教学过程，不难发现：教师对学生思维启发过程中无意地陷入了“隐性牵引”之中。师生在解题分析中的交流中，教师提问环环相扣，密不透风，学生回答准确流畅､了无破绽。看似真实的师生互动对话，实则是低层次､低价值､低效率的师生问答，看似引领学生共同经历思维过程，实则教师一语牵引学生思维过程，学生亦步亦趋，不感越雷池半步。
这样的思维启发过程，久而久之，学生将丧失自主解读数学文本的能力，即使头脑聪慧的学生，也会陷入教师预设好的思考路径中，形成思维过程的“路径依赖”，不再会萌发富有个性的创新解题思路与方法。学生掌握的是如何僵化地套用模式，进行数量的查找与替换，简单解题思路的复制与粘贴。可以说，这个教学环节预设的失误就在于教师理念的落后，不相信学生的能力，放不开手脚，一味地牵引学生的思维过程。
在这个教学过程中，学生走进教师预设好的师生问答中，因而学生也就无法充分体验探索的艰难与快乐､思维的困惑与恍然，合作的分歧与共振。这样的教学，教师让学生享用了一道低效的“思维训练快餐”，而无法实现让师生共同经历探索数学､建构数学､感悟数学的过程。
对这一教学环节，可以这样设计：
师：请同学们自主阅读例1，边读边思考以下几个问题。
教师出示阅读提示：
1.通过读题，你读出题中有几个量，分别是什么？
2.这些量可以建立怎样的数量关系式？
3.根据已有的经验，你觉得这道题可以用什么方法解题？为什么？
4.你有其他解法吗？
这样的设计可以充分发挥学生的思维主体地位，又能体现教师思维引路的作用。教师让学生自主的解读题意，寻找数量间的数量关系式，寻求解答问题的方法，尝试自主的数学建构，有效地帮助学生克服“路径依赖”，从而真正实现教师对学生思维过程的有效引领。