首页 -> 2007年第6期
数学试题要体现“三维”目标
作者:韦波富
一、 知识与技能的考查重在理解
数学课程标准在知识与技能总体目标中指出,“要经历……过程,掌握……”我们解读为数学的知识与技能应是理解基础上的掌握。命题时一方面要考查学生知识、技能的掌握程度,更重要的是要考查学生对知识的理解情况。只有理解了的知识,运用才会自如。
例1如果X2=6X(X≠0),那么X等于多少?
该题考查的不是学生解方程的技能,主要考查学生对等式性质以及平方数的理解,针对性比较强。可以将等式两边同时除以X,得X=6。也可以根据X2的意义来解答,左边X2=X•X,右边6X=X•6,比较等号的左右两边可以得出X=6
例2甲杯里有水450克,乙杯里有水356克,现将50克糖放入甲杯,44克糖放入乙杯,这时哪杯糖水甜一些?
这是对学生百分率理解情况的考查,与以往命题不同的是没有直接要求学生求百分率,而是让学生根据实际情境,自觉运用知识解决问题。解决这样的问题要基于学生对百分数产生过程的理解,因而能对课堂教学起到一定的导向作用。
例3有a个零件(a>1),王师傅独做4小时可以完成,李师傅单独做5小时可以完成。如果两人合做,几小时可以完成?解法正确的是( )
A、a÷(4+5)B、a÷(1/4+1/5) C、1÷(1/4+1/5)
该题主要考查学生对工程问题数量关系的理解。教学中教师需要引导学生经历从具体到抽象的过程。题中零件个数用字母表示,增强了试题的信度。
例4一个圆锥的体积是圆柱体积的。如果圆柱的底面积是12平方分米,高是3分米,那么这个圆锥的底面积、高可能是多少?(请你给出三个答案填在下表中)

该题一方面考查学生对等底等高的圆柱、圆锥体积之间关系的理解,另一方面培养学生思维的辩证性,即当圆锥体积是圆柱体积的1/3时,它们可能等底、等高,也可能不等底也不等高。
二、 过程与方法的考查重在探索
“过程与方法”这一目标,要求学生“初步学会运用数学的思维方式观察、分析现实社会,去解决日常生活中和其他学科学习中的问题,增强应用数学的意识”,因此编拟的试题应以学生学过的知识和解决简单的实际问题为背景,引导学生运用数学的方法,通过探索去解决。
例1:按规律填空
37037×3=111111
37037×6=222222
37037×9=333333
37037×15=( )
()×()=999999
该题设计的意图不是考查学生基本的运算技能,而是考查学生“探索给定事物中隐含的规律”的能力。
例2坦克模型玩具是用棱长1分米的正方体盒子包装的,现在需要把24盒装成一箱,为了使包装箱的表面积尽可能小,玩具厂征集包装箱设计方案。小明设计了3种方案(见下表)。
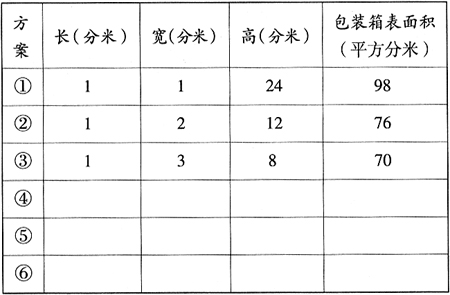
(1)请你设计3种与小明不同的方案(长、宽、高分别是1、1、24;1、24、1;24、1、1属同一种方案),将有关数据填在表格中。
(2)观察表中长、宽、高数据的变化,想一想:当长方体体积不变时,在什么情况下它的表面积最小?把你的发现写下来:___________________________________________________
(3)根据你的发现,如果要将36盒玩具装成一箱,当长是()分米、宽是()分米、高是()分米时,箱子的表面积最小。
该题所依据的知识基础是学生对体积概念的理解、空间观念的建立、表面积计算方法的掌握,所依托的探究经验是长方体体积计算方法的推导过程以及“长方形周长一定,长、宽的变化规律”的探究经历等。该题几个问题的设置循序渐进,旨在利用学生的知识基础和学习经验“引导”学生实践和探究,从中发现规律,并运用规律解决相似的现实问题。通过解答体验数学与生活的密切联系,认识到许多实际问题可以借助数学方法来解决,并可以借助数学语言来表达和交流。
例3 同学们一定对梯形面积公式的推导过程记忆犹新,你能运用这种方法求出下面物体的体积吗?(单位:厘米)
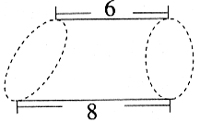
转化是一种重要的、常用的数学思想方法,在小学阶段学生经历得较多。提示语是唤起学生对梯形面积公式推导过程的回忆,是一种学法指导,同时培养学生“回顾与分析解决问题过程”的意识,引导学生调动自己的探究经历,运用转化的思想解决问题。
例4下面是欣欣百货公司去年销售游泳衣和羊毛衫的情况统计图,你能说出哪一张是游泳衣的销售统计图吗?
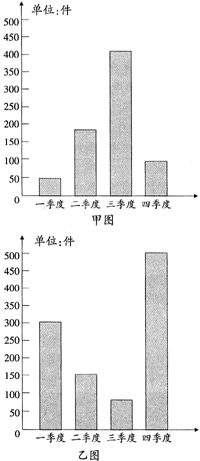
_____________是游泳衣的销售统计图。我的理由是________________________
“能解释统计结果,根据结果作出简单的判断和推测”是统计教学的目标之一。学生根据两个统计图中的信息进行分析和比较,并凭借学生已有的生活经验进行合情推理,作出判断,可以有效地考查学生对条形统计图的数据的分析能力。
三、 情感态度价值观的考查重在感悟
情感、态度、价值观是难以测量的,这一目标也不是靠做一道题就能检测出来的。但在编拟试题时要尽量“体现”这些目标,通过试题资源去熏陶,由学生去体验,通过潜在的积累而获得。
例1扬州火车站地下通道地面是用黑白两种地砖铺成的(如下图)。如果用X、Y分别表示黑白地砖的块数,那么它们之间的关系可以表示成_____________。

该题涉及到的知识点是正比例的意义。设计的主要意图是引导学生用数学的眼光看待周围的事物,用数学的方法描述现实生活中的简单现象,感受数学的存在。
例2一个圆柱形盛水容器,从里面量底面半径4分米,深6分米。现在再做一个圆柱形容器,要求容积是它的8倍,请你设计出两种方案,填在下表中。

该题是积的变化规律在解决实际问题中的巧妙运用。可以将底面半径扩大2倍,深扩大2倍,或底面
半径扩大4倍,深缩小2倍等。该题的精妙之处就是将这一知识点放在一定的生活情境中,通过方案设计形式加以呈现,可以让学生感受到数学知识在生活中的应用价值,体验数学活动的探索性和创造性。
例3润扬建筑公司有两个工程队,甲队有28人,乙队有22人,现要使甲乙两队的人数比为3:2。
(1)请你先判断下表中给出的几种方案的可行性(可行的打“√”,不可行的打“×”),再算出增加、减少或甲乙两队调整的人数,填在表格中。

(2)请你再设计一种方案,并算出结果。
有关比的知识在该题中得到了较为全面的综合运用,同时方案3和方案4需要学生根据能被3整除的数的特征作出判断。该题注意数学知识运用的实际背景,设计巧妙。学生通过对几种方案的验证、判断,领悟到不同方案的特点,感受到解决问题方法的多样性。题中“请你再设计一种方案”给了学生自主探究的空间,而方案的选择打开了学生的思路,又为自主设计提供了方法上的指导和心理上的准备,增强了学生解决问题的信心。
知识与技能、过程与方法、情感态度与价值观这“三维”目标是一个整体,能力问题以及情感、态度、价值观的问题,都是依附于知识发生、发展过程之中的,是在探索知识的过程中得以形成和发展的。命题时要以知识为载体,体现过程与方法,从而达到培养学生积极的情感、态度、价值观等目的。
责任编辑:陈国庆