首页 -> 2008年第4期
小学数学命题趋势例谈
作者:肖伟国
一、 凸现人文性
应试教育下的考试评价是“几家欢乐几家愁”。数学试卷因过分强调甄别与选拔,考试严肃有余而活泼不足,试卷缺乏人文性,使孩子们一看就产生沉重感、紧张感,这样必然会加重学生的心理负担,不利于学生发展。数学课程标准明确指出:“对学生的评价不仅要关注学生学习的结果,更要关注他们在学习生活中的变化和发展。”因此,考试评价传递给学生的是“考试是一份期盼”的人文关怀,具体体现在:首先在试卷中加入了情感激励的语言,有亲切的问候:“同学们,经过这一年的学习,你一定有不少的收获吧!下面的题目,会让你对自己的学习有一个全面的评价。”有谆谆的告诫:“仔细审题,认真答题,你就会有出色的表现,相信自己的实力。”“恭喜你做完了,是不是再检查一遍?”其次,在试卷的命题方面,还选取了一些有着丰富人文内涵的学习资源。
例1:江苏森达集团产值统计图

根据上图回答有关问题:
1.此图是()统计图。
2.2006年产值比2005年增长了()% 。如果按这个增长率推算,那么2007年的产值应是()亿元。
3.如果你是江苏森达集团的总裁看到这张统计图,对集团以后的发展有何打算?
此试题是让学生充分利用统计知识,来分析解决日常生活中的数学问题,培养学生的应用意识,同时又赋予人文内涵,让学生以集团总裁的身份,根据有关统计结果对集团以后的发展作出一个简单的规划。这样,在学生表述的基础上增加亲和力,消除学生的紧张和恐惧心理,使孩子们感到题目既有趣又轻松,缩短学生与试卷之间的距离。
二、 满足差异性
让不同的人在数学课上得到不同的发展,这是数学教学改革的新理念。在评价时关注学生的个性差异,保护学生的自尊心和自信心,就显得尤为重要。因此,命题时既要关注后进生和中等生,又要关注优等生,满足差异发展,让不同的学生数学能力都能得到展示,从而使学生的学习积极性得到保护,个性得到张扬。
例2 :家里来了一批客人,爸爸拿了34元钱给小丽去超市买雪碧。要求她买的雪碧的总体积大于13升,超市中的雪碧有两种规格(详见下表)。请你帮小丽设计出不同的购买方案。(每设计出一种正确的方案可得1分,每人至少写出3种不同的方案,多写1种另加1分,加满3分为止)
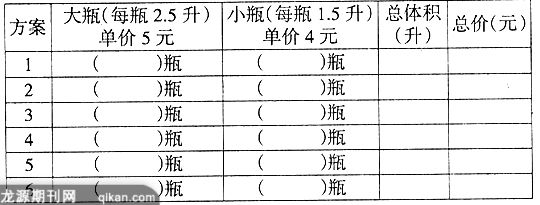
此题既有基本分又有附加分,基本分是面向全体学生,附加分是让学生针对自身情况,进行选择解答。这样的命题满足了不同学生的需要,给学生提供了一个尝试的空间。
三、 强调综合性
培养学生的综合素质能力,不仅仅是学生对学科内各知识点之间的综合运用,还应包括学科与学科之间知识的综合运用。就目前的命题来看,所选用的综合试题已经不局限于原来的“老面孔”,而是赋予新的背景,涉及历史、地理、经济、人文等社会生活的各个方面,在检测教学质量的同时,也丰富了学生的知识,激发了他们去探究新知的欲望。
例3 :下面节日同在大月的一组是()
A、劳动节建军节B、儿童节国庆节
C、元旦 教师节D、妇女节清明节
这一题不仅检测了学生对“年、月、日”的知识,特别是对一年中有哪几个月是大月的了解,还借助于全年中的一些重大节日这一背景,检测了学生对社会知识了解的程度,渗透了思想教育。
四、 注重开放性
开放性的数学问题,可为学生提供更多的思考和探索的空间,有自主创新的机会,对培养学生的创新意识,有着不可忽视的作用。这一作用已被大家所认同,一些比较开放的、有利于学生自主创新的题目,逐渐出现在学生的质量测试卷中。
例4 :一个水塘的平均水深是1.1米,小明的身高是1.3米,他不会游泳,如果小明不小心滑落塘中,他会有危险吗?()请你结合数学方面的有关知识,用一句话说明理由:()
此题中的平均水深是1.1米,所隐含的条件是多种多样的,学生可以从小明滑落水塘的地点不同来考虑,还可以从水塘池底的结构来考虑等。解答时,学生不仅能感悟到平均数的魅力,又能以数学的眼光,从现实生活中发现问题和提出问题,并探索出解决问题的有效方法和策略,表达解决问题的过程,并尝试解释探索所得到的结果,这样才能真正体现出数学的价值。
五、 突出实践性
数学源于生活,启于生活,应用于生活。应试教育下的学生学会了书本知识,却不能主动尝试着从数学的角度,运用所学的知识和方法去思考、提出或解决生活中的问题。他们缺少从事数学实践活动的机会,只能靠简单的记忆、模仿去解决书本上的一些问题,缺乏综合实践能力和创新意识。数学课程标准明确提出:“学生要通过数学实践活动了解数学与生活的广泛联系,学会综合运用所学知识和方法,解决简单的实际问题,加深对所学知识的理解,同时培养他们的实践能力和创新意识。”这就要求我们在命题时要扩大视野,在“学校数学”与“生活数学”之间架起一座桥梁,设计出实践性的试题。
例5:一个空酒瓶,不知道它的容积,给你下列材料(一只量筒、一把直尺、一个长方体形状的水槽和一些水),你能想办法知道它的容积吗?(用两种方法说明)
这是实际生活中常见的数学问题,通过解决这类问题,不但可以检测学生能否正确使用一些常见的测量工具(如直尺和量筒的使用),还可以让学生进行各种各样的探索,不断地提出问题,不断地设想解决问题的方法。在反复尝试的过程中,学生的综合实践能力和创新能力得到培养,同时也渗透了“等积代换”的数学思想。