首页 -> 2008年第7期
《用一一列举的策略解决问题》教学设计
作者:黄正威
苏教版国标本《数学》五年级上册教材第63~64页的例1、例2和“练一练”,都有用“一一列举”策略解决问题的成分在里面,但解决这些问题要综合运用各种策略,本节课打算将“一一列举”策略以板书、朗读、回顾、总结、提升等方式加以强调,达到新学之目的。
例1与学生的生活有一定距离,但我们这里几乎家家养羊,县政府把养羊作为农业支柱产业发展,五年级学生对此有所耳闻,所以我们决定保留例1。例2是订阅杂志的,对农村孩子可能比较生疏,我们决定在课堂上作简单介绍,给学生一定的背景知识。“练一练”是游戏中的问题,多数农村孩子未玩过飞镖,未见过靶盘,但为了丰富他们的课外生活,学习之前出示飞镖与靶盘,让学生见识并适当练习,我们认为是可以的,因为数学课既要让学生学习数学,又要让学生过上幸福的课堂生活。
目标预设:
1.使学生经历用列举的策略解决简单实际问题的过程,能通过不遗漏、不重复的列举找到符合要求的所有答案。
2.让学生在解决简单实际问题的过程中反思和交流,感受“一一列举”的特点和价值,进一步发展思维的条理性和严密性。
3.增强解决问题的策略意识,提高解决问题的实际能力。
重点、难点:
在实施策略的过程中,感受“一一列举”的特点和价值,是教学重点;“一一列举”策略的顿悟生成,形成学生的智慧,是本节课的教学难点。
设计理念:
1.解决学生身边的实际问题,让学生感知数学就在生活中,学习数学很有用。
2.“一一列举”的策略由学生自主探索,顿悟生成,形成智慧,而不是单一地训练学生解题的技能技巧。
3.研究学生当下以及将来的生活,与学习内容无痕对接。
设计思路:
课始复习四年级学习解决问题的策略,为迁移作准备;开门见山地揭示课题,为学生的学习定向。例1、例2和“练一练”,均分成两段教学,目的是减缓解决问题的坡度,获得解决问题的成功感。另外,学生从第一段无序列举、个别列举到第二段的有序列举、全面列举,感受到“一一列举”的特点和价值。例1、例2和“练一练”的教学,逐步放手于学生,学生从无意识地列举到有意地运用策略解决问题,实现策略教学的根本目的。课末的回顾,让学生整理新学的策略,将之纳入自己的认知结构中。练习评价自己,明白自己本节课数学学习的优点与不足,调整今后的学习,从而提高学习数学的有效性。
教学过程:
一、 谈话导入
在四年级的时候,我们曾经两次学到过解决问题的策略,是哪些策略呢?(列表的策略、画图的策略。)今天,我们继续学习——解决问题的策略。(板书课题)
二、 解决生产中的问题
1.谈话:王大叔要用18根1米长的栅栏围成一个长方形的羊圈,估计他会怎样围呢?
2.大家说了这么多的围法,真爱动脑筋。如果我问:有多少种不同的围法?又该怎么办呢?
提示:找出所有不同的围法,要讲求一些策略才行。围长方形不外乎长、宽两个要素,长、宽不同,就算不同的围法。
出示下图:

请学生把这张表画到自己本子上,并把它填完整。
实物投影:两张不同的列表形式。
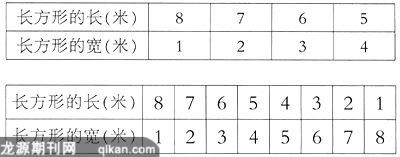
这两张表有什么相同的地方和不同的地方?要研究有多少种围法,你认为哪张表是正确的?为什么?
学生发表意见后,教师把表示长4米宽5米的长方形模型旋转90°,让学生看到长4米宽5米的长方形与长5米宽4米的长方形形状是一样的。相机贴出长8米宽1米、长7米宽2米、长6米宽3米的长方形模型。擦掉第二张表中的后4栏。
3.共有4种不同的围法。这个答案是我们采取什么策略得到的?引导学生回顾列举策略的生成过程,整体感知列举策略。
4.王大叔看了这4种围法,决定采用哪一种呢?
出示下图:
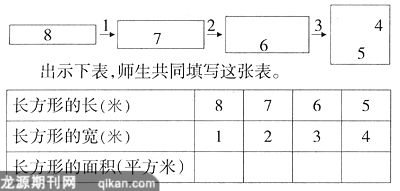
引导学生将面积与长和宽的差距联系起来考虑,同时强调长与宽的和是固定的数,我们才能一一列举。
三、 解决学习上的问题
1.明年的杂志,现在可以征订了。下面有三种杂志,最少订阅1本,最多订阅3本。你想怎样订阅?
2.出示例2
三种杂志,最少订阅1本,最多订阅3本。有多少种订阅方法?这个问题怎样解决?你准备用什么策略?
学生尝试解决。交流。
看来列举用语言叙述可以,用画表打“√”的办法也可以。运用画表打“√”的办法列举,会使你的解题思路更加清晰。
为发展学生思维的条理性,进行分类列举,分步出示例2中的表格。
3.小结:求一共有多少种不同的订阅方法,我们又运用了什么策略?再次回顾“一一列举”策略的生成与实施,感受其特点和价值。
四、 解决游戏里的问题
1.观察靶盘,找学生练习投镖。
2.如果全班每人投一次,可能会出现哪些不同的情况?
3.出示“练一练”:
一张靶纸共三圈,投中内圈得10环,投中中圈得8环,投中外圈得6环。小明投中两次,可能得到多少环?要求列举出所有可能的答案,独立完成。
4.交流,你是怎样列举的?出示:

共同校对。按照顺序列举,一共有多少种不同的环数?
(交流时明确:8+8=16,10+6=16,算同一种环数。)
五、 教学总结
这节课好玩吗?你有什么收获?对自己有怎样的评价?