首页 -> 2009年第1期
让数学文化丰润数学课堂
作者:章亚萍
一、 在概念教学中揭示文化底蕴
在概念教学中,我们要充分挖掘教材所蕴含的文化内涵,适当插入一些有关数学发现与数学史的知识,如介绍某一个数学问题解决的艰辛历程,介绍古今中外的数学史料等,以还原数学概念的内在生命力量,彰显概念的文化价值。
1.在追本溯源中展现厚重。历史不仅可以给出一种确定的数学知识,还可以给出相应知识的创造过程。对这种创造过程的了解,可以使学生体会到一种活的、真正的数学思维过程。我们应该结合具体的教学内容,让数学史走进课堂,使学生更好地了解、学习和研究数学,进一步体验数学概念沉淀下的丰富内涵。如四年级上册“数的产生”一课,通过前面的学习,学生已经知道了亿以内数的认、读、写、大小比较,计数单位、数位、数级等知识,获得了丰富的数的感知,但还缺乏对数背后蕴藏着的丰富的数学历史与数学文化的深刻认识。因此,在教学这一内容时,我们可以把数的产生过程作为学习内容的凝聚核,把数的产生过程、各国的数文化、与数有关的诗歌、对联等内容有机地组成一个整体展示给学生,这样可以使学习的辐射面广、信息量大,让学生充分地体验与感受数的魅力。
2.在引经据典中释放活力。对于一个新的数学概念和新的数学知识,我们可以从追寻历史故事或史实引入,这样可以激发学生学习兴趣,使学生不再感到数学概念的枯燥,而且十分有助于培养他们的探索精神,帮助他们理解与掌握所学的内容。如在六年级“比的意义”教学中,教师先出示了10个大小形状各异的长方形,要求学生选出自己认为最美的长方形。结果,学生不约而同地选择了同样的两个长方形(这两个长方形的长宽之比均为“黄金分割比”)。正当同学们为彼此之间的不谋而合而倍感费解时,教师不失时机地引入了1000多年前,德国心理学家费希纳做同样实验的数学典故。学生纷纷质疑:究竟是什么原因导致这些长方形被大家公认为是最美的呢?其中蕴涵着怎样的奥秘?于是,教师趁机揭示研究主题。就这样,一次有趣的课堂实验,一个简短的科学典故,使得枯燥的数学教学感染上了浓郁的文化气息。在这里,数学教学不再是单向的知识传递,而是生动的文化交流。
3.在追寻足迹中踏雪寻梅。数学家在探索、论证、创造过程中折射出的执着、严谨、超越等敬业品质和民主精神等,见证着数学更为深沉的文化力量。在课堂教学中,我们可以适时地将一些数学家的探索故事介绍给学生,使学生在人格上受到熏陶。如在解决“等差数列求和”的问题时,教师出示“1+2+3+4+5+6+……+98+99+100”这道题,让学生独立思考解决的办法。当学生觉得困难时,教师不失时机地向学生介绍了伟大数学家高斯在八岁的时候就以惊人的速度和最巧妙的方法计算出这道题的故事。每一位学生都为之而惊叹,他们被高斯善于思考、分析、观察、钻研的数学精神而深深打动。每一位学生都深刻地认识到思考的力量是无穷的,思考不仅可以找到解决问题的策略,更重要的是可以带来学习的快乐。
二、 在解决问题教学中感悟思想方法
数学思想方法是最基本的数学文化素养,是数学思维的结晶和概括,是解决数学问题的灵魂和根本策略。我们应敏锐地予以捕捉、判断、放大、外化潜伏于许多看似普通的数学知识、技能、问题中的方法、思想和策略,并在日常的教学与活动中适时地加以渗透,充分挖掘数学的丰富文化内涵。
1.在知识形成中感受美妙。对数学而言,知识的形成过程实际上也是数学思想和方法的发生过程。教学时如果处理不当,则会使学生陷入机械记忆、单纯模仿、反复操练的窠臼。我们应使学生置身于规则发生、发展、形成过程和结论的推导过程,在引导他们亲历观察、猜想、验证、建模、应用等数学活动中渗透数学思想和方法,进而获得一种更有力度、充满张力的数学思考以及触及心灵的精神愉悦。如在教学进位加法时,教师放手让学生探索33+37的笔算方法。没想到,有不少学生选择了从十位加起,过程如下:

教师并没有草率否定,也没有立即纠正,而是引导学生比较两种不同计算规则,学生在比较、感悟中,不仅掌握了“从个位加起”的方法,更深化了对这一规则合理性的认识,感受到计算规则丰富和确定的辩证统一,体验到规则生成过程中丰富的数学思考。
2.在策略探究中体验博大。掌握科学的数学思想方法对提升学生的思维品质,对后继学习,对其它学科的学习,乃至对学生的终身发展都具有十分重要的意义。在解决问题教学中,我们应有意识地引导学生掌握有效的解题策略,如“综合与分析”、“画图与列表”、“倒推”、“假设”、“枚举”、“转化”等,让学生在解决问题的过程中感受数学文化的真正价值。如“求一个数比另一个数多几”这类题的数量关系对二年级学生来说较为抽象。我们可以这样设计:①出示:小明家鸡有5只,鸭有7只,鸭比鸡多几只?提供解题策略:画图或利用○、△摆一摆(学生在摆、画的过程中领会一一对应的思想);②将“5”、“7”改成“50”、“70”。学生在感受示意图直观形象的同时,发现当数据较大时有局限性,从而再出示线段图帮助学生理解解题思路。这样渗透了数形结合思想,把抽象内容的数量关系视觉化、具体化、形象化,化深奥为浅显,使学生领悟到数学思想方法的博大精深。
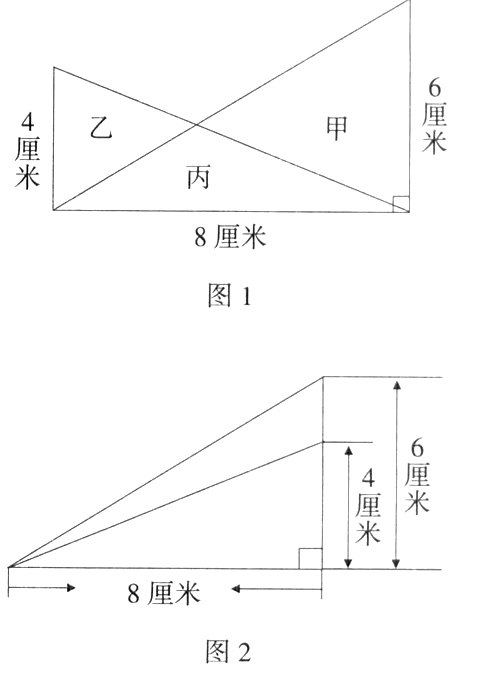
3.在问题解决中积淀精巧。数学问题的解决过程就是用“不变的数学思想和方法去解决不断变换的数学问题”。方法、策略、思想却常常以更为内敛、潜在的方式沉积于学生内心深处,成为学生进行思考的重要支撑。因此,在问题解决中渗透数学思想和方法,不仅可以加快和优化问题解决的过程,而且还可以达到会一题而通一类的效果,提高学生独立获取知识和解决问题的能力,体验数学思维带来解题的乐趣。如解答“甲、乙三角形的面积相差多少平方厘米?”这道题时,(如图1)。
大部分学生按一般方法思考,即先求出甲、乙三角形的面积,然后再相减求差。但从已知条件来看,无法求出这两个三角形的面积。这时教师引导学生用运动的观点来观察、分析图形,学生发现:这个组合图形可看成是由两个直角三角形交叉重叠组成,丙是重叠部分。如果改变一下两个直角三角形的摆放位置,即变成图2。要求甲和乙三角形面积的差,就转变成求(甲+丙)与(乙+丙)三角形面积的差,即求图2中钝角三角形的面积。学生恰当地运用已知条件将问题逐步转化,凸显出问题的本质,看清了问题的实质,问题也就迎刃而解。
三、 在综合应用中体验应用价值
在课堂教学中,我们要善于挖掘生活中、各学科中的数学实例,使学生体会数学与人类社会的密切联系,
初步学会运用数学的思维方式去观察、分析现实社会,去解决日常生活中的问题,体验数学的科学价值、应用价值。
1.在生活实际中体会。课标指出:“教师应充分利用学生已有的生活经验,随时引导学生把所学的数学知识应用到现实中去,解决身边的数学问题,以体会数学在现实生活中的应用价值。”教学中,我们要找准每课时内容与学生生活实际的“切合点”,引导学生用数学眼光去观察生活,从数学的角度收集生活中蕴涵的大量数学信息,从中提炼出数学问题,体会数学知识在实际生活中的作用以及与生活的密切联系。如在学习“三角形稳定性”后,引导学生去观察生活中哪些地方应用了此定理。在教学“24时记时法”时,可让学生制定出自己每天的作息时间,看看怎样安排比较合理、科学。通过这种方法使学生进一步了解数学在现实生活中的广泛应用,增强学生应用知识解决实际问题的意识,调动学生学习兴趣和参与积极性,体验其中无穷的乐趣。
2.在学科渗透中领略。数学教学应使学生感受到数学文化与其他文化的相互渗透和融合,感受数学的无处不在。因此,我们应走出数学“金字塔”,以开放的姿态展示其与自然、社会及各门学科的联系,充分放大数学所蕴含的文化特性。在课堂教学中,我们可以尝试着与语文、科学、体育、美术等学科沟通联系,一方面可以让其他学科知识充实数学课堂,另一方面可以促进各学科知识的整合。教师可以为学生提供真实的、与其他学科密切联系的、学生感兴趣的数学活动和问题,使学生在探索和讨论的过程中,开阔思路,激活思维,加强数学的应用意识和应用能力,使学生进一步理解数学的价值和意义。
3.在课外实践中升华。在课外实践中我们可以指导学生开展小课题研究,使学生在实践中再次感受数学文化的应用价值,这对于培养学生独立观察、思考和解决问题的积极性和主动性以及创新精神和实践能力都有积极的推动作用。更重要的是,学生通过课外实践可以受到人格品行的教育。如在学习了“统计”与“大数的认识”后,可以组织学生开展小课题研究,如“白色污染——塑料袋”。要求:了解塑料袋在生活中的作用,包括益处与弊端。采访周边的群众,听听他们对白色污染的看法。收集自家每天每人平均用塑料袋的个数,全班同学每天用塑料袋的个数,并由此推导出全村、全镇、全国每天每人平均用塑料袋的个数,制成统计表。再计算出全国一星期、一个月、一年所用塑料袋的个数。形成小报告后在全班畅谈感受。这既丰富了知识背景,拓展了知识的应用领域,又培养了学生处理和正确运用信息的能力,提高了学生运用数学知识解决实际问题的能力,使学生在生活实践中进一步感受数学的应用价值。
(参考文献本刊略)