首页 -> 2009年第1期
《用倒推的策略解决问题》教学设计
作者:陈 蕾
教学目标:
1.使学生通过分析具体情境中的实际问题,体验“倒过来推想”的策略解决特定问题的价值,初步学会运用“倒过来推想”的策略寻找解决问题的思路,并能根据问题的具体情况确定合理的解题步骤。
2.使学生在对解决实际问题过程的不断反思中,进一步发展分析、综合和进行简单推理的能力。
3.使学生进一步积累解决问题的经验,增强解决问题的策略意识,获得解决问题的成功体验,提高学好数学的信心。
教学重点:
学会运用“倒过来推想”的策略寻找解决问题的思路,并能根据问题的具体情况确定合理的解题步骤。
教学准备:
挂图 课件水杯
教学过程
一、 教学例1
1.呈现问题。
(1)出示“原来的”两杯果汁,并出示条件“两杯果汁共400毫升”。
提问:如果把甲杯中的40毫升果汁倒入乙杯,这两杯果汁的数量分别会发生怎样的变化?
(2)学生回答上述问题后进行实际的操作演示,让学生发现不仅甲杯减少了乙杯增加了,而且甲杯和乙杯正好同样多。
(3)回顾操作过程,出示例题中条件部分的完整示意图,提出问题:原来两杯果汁各有多少毫升?
2.解决问题。
(1)提问:把甲杯中的40毫升果汁倒入乙杯后,两个杯子里的果汁总量有没有变化?现在每个杯子里各有多少毫升果汁?
(2)小组讨论:知道了现在两个杯中的果汁数量,可以怎样求原来两个杯中的果汁数量?可以用怎样的方法来解决?
(3)在学生提出“再倒回去看一看”时,追问:如果把乙杯中的40毫升果汁再倒回甲杯,两个杯中的果汁数量又会发生怎样的变化?
(4)学生画图后,组织展示、交流,并相机呈现教材提供的第二组示意图。
引导学生认识到“再倒回去”后,甲杯在200毫升的基础上,增加了40毫升;乙杯在200毫升的基础上,减少了40毫升。
(5)小结:看来“再倒回去”是个好办法,用这个办法我们很容易就能想到原来两个杯子里各有多少毫升果汁。
3.填表回顾,加深对“倒过来推想”的体验。
(1)回想一下,我们刚才是怎样解决这个问题的?你能按照解题的过程将课本中的表格填写完整吗?要求边填边想表中的每个数据各是怎样推算出来的。
(2)提问:在解决这个问题的过程中我们运用了哪些策略?你认为“倒过来推想”的策略有什么特点?
学生讨论后,揭示课题并板书:用倒推的策略解决问题。
二、 教学例2
1.出示例2,让学生读题后,再要求说说题目的大意。提问:用什么方法可以将题目的意思更清楚地表示出来?
2.在学生讨论后,指出:可以按题意摘录条件进行整理。出示:
原有?张→又收集了24张→送给小军30张→还剩52张
提问:你能根据上图再说说题目的大意吗?要求小明原来有多少张邮票,你准备用什么策略来解决?
3.明确可以用“倒过来推想”的策略解决问题后,提出:你能仿照上图的样子,表示出“倒过来推想”的过程吗?
学生尝试画出倒推的示意图后,交流:
原有?张← 去掉收集的24张← 跟小军要回30张←还剩52张
要求根据上图写出倒推后每一步的结果,再让学生综合“倒过来推想”的过程列式解答。
4.简化思路:根据小明邮票张数的变化情况,也可以画出下面的流程图:

同时启发学生思考:有没有其他的方法?(转化出“又搜集的比送出的少6张”,可以得出什么算式?还可以列方程来解答。)
5.检验:要求学生根据答案和“小明邮票张数”的变化情况顺推过去,看看剩下的是不是52张。在顺推和倒推的对比中,进一步认识倒推策略。
6.反思:解决上面这个问题时,是怎样运用“倒过来推想”的策略的?你认为适合用“倒过来推想”策略来解决的问题有什么特点?
三、 应用巩固
1. 练一练。
学生各自读题。提问:你打算用什么样的策略解决这个问题?“拿出画片的一半还多1张送给小明”是什么意思?你能换种说法表示这样的意思吗?
画一画:
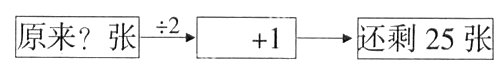
学生解题后,组织交流,重点让学生说说推想的过程。
2.填一填。
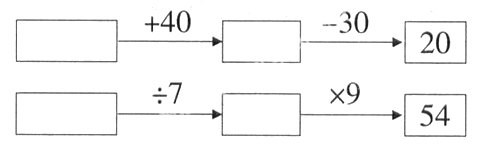
3.想一想。
(对话)一位旅行者看到牧羊人在放牧,问他:“你这群羊有多少只?”牧羊人回答:“把我这群羊的只数减去7,除以5,再加上8,乘以4,正好是100。请你算算,我有多少只羊?”
四、 课堂作业
做练习十六的第1、2题。
要求学生借助列表或者画流程图的方法整理信息,自主解题。
五、 全课小结
通过这节课的学习,你有哪些收获和体会?
游戏解密。你知道老师是怎样猜数了吧?
【设计说明】策略的学习,不能脱离解决问题的过程。有人说策略是问题解决的副产品。在把问题的最终解决作为目的时,策略的总结确实在其次,然而这从数学学习的发展目标来看又是本末倒置的。问题的解决只是数学学习的必要途径,不是学习的归宿。知识的背后是方法,方法的背后是思想。所以说,策略的学习基于解决问题,又不能囿于解决当前问题。“倒过来推想”是一种特殊策略,是特定问题情境下解决问题的策略,由于这种特定的问题情境比较常见。通常已知某种数量或事物按照明确的方法和步骤发展、变化后的结果,又要追溯它的原始或起始状态,就需要这种策略,学习这种策略,不仅丰富学生的策略模型积累,而且可以在更大范围中培养学生的思维灵活性和深刻性。
在这个教学设计中,先用有趣的猜数游戏引发学生的兴趣,唤醒学生从数学的角度来解密。在例题的学习中,分两个层次来彰显策略:首先是例1的初步感受,使学生走出混沌;其次是例2的初步运用,促使学生思维更加明朗和深刻。在交流其他解法中整合以往学习的解决问题的策略应用,检验环节也能在顺推和倒推的对比中进一步认识倒推的策略。在巩固阶段,紧扣学生刚刚认识的“倒过来推想”策略集中强化,加深学生对策略的理解和掌握,逐步达到自主自觉运用策略的境界。整个设计立足数学素养的整体建构,从问题回馈策略,又从策略服务问题,前后呼应,一气贯通。