首页 -> 2008年第9期
树立数学建模意识培养问题解决能力
作者:杨秀芹 马晓平
一、数学建模与数学建模意识
所谓数学模型,是指对于现实世界的某一特定研究对象,为了某个特定的目的,在做了一些必要的简化假设,运用适当的数学工具,并通过数学语言表述出来的一个数学结构,数学中的各种基本概念,都以各自相应的现实原型作为背景而抽象出来的数学概念。
具体的讲数学模型方法的操作程序大致上为:
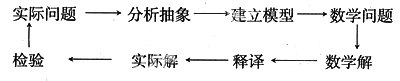
培养学生运用数学建模解决实际问题的能力关键是把实际问题抽象为数学问题,必须首先通过观察分析、提炼出实际问题的数学模型,然后再把数学模型纳入某知识系统去处理。这不但要求学生有一定的抽象能力,而且要有相当的观察、分析、综合、类比能力。学生的这种能力的获得不是一朝一夕的事情,需要把数学建模意识贯穿在教学的始终,也就是要不断地引导学生用数学思维的观点去观察、分析和表示各种事物关系、空间关系和数学信息,从纷繁复杂的具体问题中抽象出我们熟悉的数学模型,进而达到用数学模型来解决实际问题,使数学建模意识成为学生思考问题的方法和习惯。
二、构建数学建模意识的基本途径
1.为了培养学生的建模意识,数学教师应首先需要提高自己的建模意识。这不仅意味着我们在教学内容和要求上的变化,更意味着教育思想和教学观念的更新。数学教师除需要了解数学科学的发展历史和发展动态之外,还需要不断地学习一些新的数学建模理论,并且努力钻研如何把数学知识应用于现实生活。北京大学附中张思明老师对此提供了非常典型的事例:他在大街上看到一则广告:“本店承接A1型号影印。”什么是A1型号?在弄清了各种型号的比例关系后,他便把这一材料引入到初中“相似形”部分的教学中。这是一般人所忽略的事,却是数学教师运用数学建模进行教学的良好机会。
2.数学建模教学还应与使用教材结合起来研究。教师应研究在各个教学章节中可引入哪些模型问题,如讲导数时可通过物理学中的速度问题引入,其余的相关问题都可以放入这个模型中来解决;而质量问题、河流的流量问题则可结合在积分教学中。要经常渗透建模意识,这样通过教师的潜移默化,学生可以从各类大量的建模问题中逐步领悟到数学建模的广泛应用,从而激发学生去研究数学建模的兴趣,提高他们运用数学知识进行建模的能力。
3.注意与其他相关学科的关系。由于数学是学习其他自然科学以至社会科学的工具,而且其他学科与数学的联系是相当密切的。因此我们在教学中应注意与其他学科的呼应,这不但可以帮助学生加深对其他学科的理解,也是培养学生建模意识的一个不可忽视的途径。例如教了正弦函数后,可引导学生用模型函数y=Asin(wx+Φ)写出物理中振动图像或交流图像的数学表达式。这样的模型意识不仅仅是抽象的数学知识,而且将对他们学习其他学科的知识以及将来用数学建模知识探讨各种边缘学科产生深远的影响。
4.在教学中还要结合专题讨论与建模法研究。我们可以选择适当的建模专题,如“代数法建模”、“图解法建模”、“直(曲)线拟合法建模”,通过讨论、分析和研究,熟悉并理解数学建模的一些重要思想,掌握建模的基本方法。甚至可以引导学生通过对日常生活的观察,自己选择实际问题进行建模练习,也正所谓“学问之道,问而得,不如求而得之深固也”。
三、把构建数学建模意识与培养学生创造性思维过程统一起来
在诸多的思维活动中,创新思维是最高层次的思维活动,是开拓性、创造性人才所必须具备的能力。麻省理工学院创新中心提出的培养创造性思维能力,主要应培养学生灵活运用基本理论解决实际问题的能力。由此,我认为培养学生创造性思维的过程有三点基本要求。第一,对周围的事物要有积极的态度;第二,要敢于提出问题;第三,善于联想,善于理论联系实际。因此在数学教学中构建学生的建模意识实质上是培养学生的创造性思维能力,因为建模活动本身就是一项创造性的思维活动。它既具有一定的理论性又具有较大的实践性;既要求思维的数量,还要求思维的深刻性和灵活性,而且在建模活动过程中,能培养学生独立,自觉地运用所给问题的条件,寻求解决问题的最佳方法和途径。而这些数学能力正是创造性思维所具有的最基本的特征。
1.发挥学生的想象能力,培养学生的直觉思维
众所周知,数学史上不少的数学发现来源于直觉思维,如笛卡尔坐标系、费尔马大定理、歌德巴赫猜想、欧拉定理等,应该说它们不是任何逻辑思维的产物,而是数学家通过观察、比较、领悟、突发灵感发现的。通过数学建模教学,使学生有独到的见解和与众不同的思考方法,如善于发现问题,沟通各类知识之间的内在联系等是培养学生创新思维的核心。
例:今有甲、乙、丙、丁要完成四项任务a、b、c、d,已知工人甲能胜任b、c两项任务;工人乙能胜任a、b、d三项任务;丙能胜任a、c两项任务;丁能胜任a、c两项任务。给出一种安排方案,使每个工人各完成一项他们能胜任的任务。
分析:这是一个实际应用题,按要求,需求出一个一对一的分配方案,由此联想到图论中的匹配问题,这样可以使问题得到简化,从而得到解决。这里,匹配作为建模的对象恰到好处地体现了题中各个量之间的关系。反映了学生敏锐的观察能力与想象能力。如果没有一定的建模训练,是很难“创造”出如此简洁、优美的解法的。
2.构建建模意识,培养学生的转换能力
恩格斯曾说过:“由一种形式转化为另一种形式不是无聊的游戏而是数学的杠杆,如果没有它,就不能走很远。”由于数学建模就是把实际问题转换成数学问题,因此如果我们在数学教学中注重转化,用好这根有力的杠杆,对培养学生思维品质的灵活性、创造性及开发智力、培养能力、提高解题速度是十分有益的。
3.以“构造”为载体,培养学生的创新能力
“一个好的数学家与一个蹩脚的数学家之间的差别,就在于前者有许多具体的例子,而后者则只有抽象的理论。”
我们前面讲到,“建模”就是构造模型,但模型的构造并不是一件容易的事,又需要有足够强的构造能力,而学生构造能力的提高则是学生创造性思维和创造能力的基础:创造性地使用已知条件,创造性地应用数学知识。
四、结束语
综上所述,在数学教学中构建学生的数学建模意识与素质教学所要求的培养学生的创造性思维能力是相辅相成、密不可分的。要真正培养学生的创新能力,光凭传授知识是远远不够的,重要的是在教学中必须坚持以学生为主体,不能脱离学生搞一些不切实际的建模教学,我们的一切教学活动必须以调动学生的主观能动性,培养学生的创新思维为出发点,自觉地在学习过程中构建数学建模意识,只有这样才能使学生分析和解决问题的能力得到长足的进步,也只有这样才能真正提高学生的创新能力,使学生学到有用的数学。
参考文献
[1] 沈文选编著.数学建模.长沙:湖南师范大学出版社,1999.7.
[2] 中国教育学会中学数学教学专业委员会编.面向21世纪的数学教学.杭州:浙江教育出版社,1997.5.
[3] 胡炯涛,张凡编著.中学数学教学纵横谈.济南:山东教育出版社,1997.12.
(责任编辑刘永庆)