首页 -> 2006年第12期

中考数学压轴试题的新走势

作者：安国钗

　　近两年的中考,在新课程改革的理念指导下,题型灵活､设计新颖､富有创意的压轴试题如雨后春笋般涌现,其中一类以轴对称､平移､旋转､翻折等图形变换与二次函数相结合的试题更是成为中考压轴大戏的主角,现例举2006年中考压轴题评析如下｡
　　
　　一､ 图形翻折与二次函数相结合
　　
　　[评析]此题把三角形的折叠放到坐标系中来研究,综合考察了折叠的性质,求点的坐标,求抛物线的解析式,直角三角形的判别等知识,既是代数与几何的有机结合,又有运动与静止的辩正统一,有梯度,又有一定的难度,需要学生具有扎实的基本功和综合运用数学知识解决问题的能力｡其中第(3)小题还要能够根据条件和图形的特点进行合理猜想,运用反证法来合理验证,体验了新课程的理念｡
　　
　　二､ 图形旋转与二次函数相结合
　　
　　例2.[宜昌]如图,点O是坐标原点,点A(n,0)是x轴上一动点(n<0)｡以AO为一边作矩形AOBC,使OB=2OA,点C在第二象限｡将矩形AOBC绕点A逆时针旋转90°得矩形AGDE｡过点A得直线y=kx+m(k≠0)交y轴于点F,FB=FA｡抛物线y=ax²+bx+c过点E､F､G且和直线AF交于点H,过点H作x轴的垂线,垂足为点M｡
　　(1)求k的值;
　　(2)点A位置改变使△AMH的面积和矩形AOBC的面积比是否改变?说明你的理由｡
　　解析:(1)根据题意得B(0,-2n),
　　 当x=0时,y=kx+m=m, ∴ F坐标为(0,m)
　　 而FB=-2n-m,又在Rt△AOF中,
　　
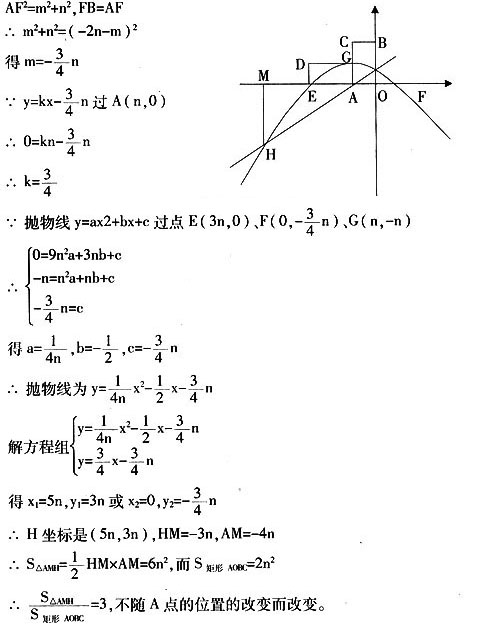
　　[评析]此题通过矩形的旋转,考查了旋转变换,解直角三角形,求点的坐标,待定系数法求函数解析式,代数法求图形的面积等知识,有机地把代数､几何知识在坐标系中,融猜想与证明,既让学生欣赏了图形变换之美,又在数学探究过程中感悟了数学的动中取静,变中不变的辩证思想｡
　　
　　 三､ 图形平移与二次函数相结合
　　
　　[评析]课改后,圆的知识虽然做了删减,在中考压轴题中失去了霸主地们,但圆与二次函数的综合仍是命题者关注的热点之一｡此题以直线与圆的几种位置关系为背景,以平移中的动圆为载体,巧妙地把圆､四边形的面积､三角形的全等等几何内容与二次函数的知识相联系,解决运动型几何最值问题,渗透了数形结合思想,分类讨论思想,具有很强的探索性｡
　　
　　四､ 轴对称变换与二次函数相结合
　　
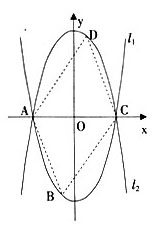
　　例4.[烟台]如图,已知抛物线L₁∶y=x²-4的图像与x有交于A､C两点,
　　(1)若抛物线L₁与L₂关于x轴对称,求L₂的解析式;
　　(2)若点B是抛物线L₁上的一动点(B不与A､C重合),以AC为对角线,A､B､C三点为顶点的平行四边形的第四个顶点定为D,求证:点D 在L₂上;
　　(3)探索:当点B 分别位于L₁在x轴上､下两部分的图像上时,平行四边形ABCD的面积是否存在最大值和最小值?若存在,判断它是何种特殊平行四边形,并求出它的面积;若不存在,请说明理由｡
　　解析:设L₂的解析式为y=a(x-h)²+k
　　 ∵ L₂与x轴的交点A(-2,0),C(2,0),顶点坐标是(0,-4),L₁与L₂关于x轴对称｡
　　
　　 ∴ L₂过A(-2,0),C(2,0),顶点坐标是(0,4)
　　 ∴ y=ax²+4
　　 ∴ 0=4a+4得 a=-1
　　 ∴ L₂的解析式为y=-x²+4
　　(2) 设B(x₁,y₁)
　　 ∵ 点B在L₁上
　　 ∴ B(x₁,x₁2-4)
　　 ∵ 四边形ABCD是平行四边形,A､C关于O对称
　　 ∴ B､D关于O对称
　　 ∴ D(-x₁,-x₁2+4)
　　 将D(-x₁,-x₁2+4)的坐标代入L₂∶y=-x²+4
　　∴ 左边=右边
　　∴ 点D在L₂上
　　(3) 设平行四边形ABCD的面积为S,则
　　 S=2×S△ABC=AC×│y₁│=4│y₁│
　　 a. 当点B在x轴上方时,y₁＞0
　　 ∴ S=4y₁,它是关于y₁的正比例函数且S随y₁的增大而增大,
　　 ∴ S既无最大值也无最小值
　　 b. 当点B在x轴下方时,-4≤y₁＜0
　　 ∴ S=4y₁,它是关于y₁的正比例函数且S随y₁的增大而减小,
　　 ∴ 当y₁=-4时,S有最大值16,但他没有最小值
　　 此时B(0,-4)在y轴上,它的对称点在D也在y轴上
　　 ∴ AC⊥BD
　　 ∴ 平行四边形ABCD是菱形
　　此时S_最大=16
　　[评析]这种“动点与坐标几何相结合”的综合性试题,将几何图形置于一个美丽的轴对称图形中,让动点带动图形的运动,从中探究图形的位置和性质特征,运用函数与几何知识进行探究数学问题,具有开放性､探索性､实践性､创造性,是一道平中见奇､奇而不偏､独具匠心的压轴佳题｡
　　分析以上几例,我们不难发现新课程下中考压轴试题的新走势;以直角坐标系和函数为载体,融代数､几何为一体,在几何图形的操作变换过程中感悟数学知识,体验数学规律,突出对考生的发散思维能力､探究能力､创新能力､综合运用能力等方面的考查,由此也给我们的教学带来一些新的启示｡
　　1､认真学习并贯彻新课程标准,进一步厘清新教材中重点知识之间的内在联系｡纵观这两年的中考试题,新增添的“图形与变换”､“统计与概率”､“视图与投影”等教学内容,都已成为中考的新贵,命题的热点｡所以,我们在教学过程中一定要加强对新课程标准的学习,对删减､增添的内容及教学要求做到胸有成竹,构建一套科学实用的新课程下的知识结构体系,这样,我们的教学就能做到有的放矢,减轻学生负担,提高教学效益｡
　　2､深化对基础知识的理解,重视知识间的内在联系,加强对学生知识整合能力的培养,提高综合应用知识解决问题能力｡我们要立足课本,以基本知识､基本方法､基本技能为主,多层次､多角度､立体化地处理教材,应用教材,对支撑学科知识的重点问题,要多引导学生学会融会贯通､举一反三｡同时,我们要培养学生及时反思和总结的良好习惯,学完每一节课,每一章内容后都要及时反思:问题的解决是否存在漏洞,是否还有其他路径,能否进行变式､类比,能否推广等,并及时进行归纳总结,把知识穿成线,织成网,横向联系,纵向发展,在理性思维中培养学生综合运用知识的能力｡
　　3､教学过程中注意对学生动手实践能力和空间想象能力的培养｡新课标下的中考加强了对学生动手实践能力､空间想象能力的考查,图形的运动变换思想是近年中考的热点｡因此,我们平时教学中要多为学生创设动手实验,操作演练的机会,让学生多做几何模型,进行展开､折叠､平移､旋转等教学实践活动,从中培养学生的图形识别能力､动手操作能力､空间想象能力,加强对图形性质､内涵的深入认识,掌握图形变换､动静结合､变与不变的规律,培养学生“透过现象看本质”的洞察能力,提高对中考综合性试题的解题信心和解题能力｡
　　(责任编辑 刘永庆)