首页 -> 2007年第7期
我国宏观特殊教育系统的系统动力学研究
作者：石学云 高 丽
2.5 特殊教育在校学生数〔dt〕与特殊教育毕业生数〔et〕的回归分析
这组关系与上组类似，因果决定关系是明显的，但拟合程度一般，如下表：
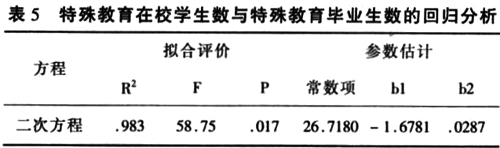
以dt为自变量，et为因变量建立方程，决定系数R2=0.983，作拟合优度检验，方差分析表明：F=58.75，P=0.017，拟合度一般，二次方程为：et=26.7180-1.6781dt-0.0287dt2。
正如前面所分析的特殊教育在校学生数的变化可能除了由专任教师数决定外，还可能有其自身的发展规律。另外，在选取特殊人群每万人口的文化程度分布指标时，我们以历年特殊学校的毕业生数为其替代指标，所以曲线拟合的效果也受到了一定的影响。
2.6 特殊教育毕业生数〔et〕与人均GDP〔at〕的回归分析
比较各种曲线回归的效果，可以看出二次曲线回归的拟合度相对较好，但因果关系和拟合度都不如前面各组，整理如下表：
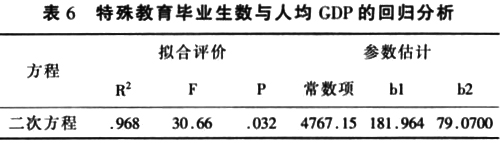
以et为自变量，at为因变量建立方程，决定系数R2=0.968，作拟合优度检验，方差分析表明：F=30.66，P=0.032，拟合度一般，二次方程为：at=4767.15+181.964et+79.0700et2。
这组数据是各组数据中拟合度最不好的一组，而在普通教育中，每万人口的文化程度的不同分布与人均GDP的拟合度很好。这一方面体现出特殊人群接受适当教育后的确对社会的发展做出了贡献，特殊人群自立后对社会的贡献，应该不仅包括其自身对经济和社会的贡献，同时也应该包括他们的自立使得身边的照顾者得以解放出来，从而为社会做出贡献。另一方面，也表明特殊学校的毕业生对人均GDP的影响是比较复杂的，职业化的特殊人群在社会中仅占非常少的比例，就整个社会的GDP发展而言，他们所起到的贡献程度也相对较少；同时，社会为特殊人群所提供的职业范围、性质、转换机会与普通人群差距较大，这也极大程度地限制了特殊人群的职业化。
3 宏观特殊教育系统的系统动力学分析
系统动力学(System Dynamics，简称SD) 是由美国麻省理工学院(MIT)的福瑞斯特(J．W．Forrester)教授于1956年提出的。系统动力学是一门分析研究信息反馈系统的学科，也是一门认识系统问题和解决系统问题的交叉综合学科。系统动力学对问题的理解，是基于系统行为与内在机制间的相互紧密的依赖关系，并且通过数学模型的建立过程，逐步发掘出产生变化形态的因、果关系，并通过计算机仿真运算，获得对真实系统的跟踪，实现社会系统的战略与策略实验。
宏观特殊教育系统是整个社会系统的一个子系统，该系统内部各要素之间、系统与外界环境之间必然相互影响、相互作用。因此，借鉴系统动力学的研究理念，研究宏观特殊教育系统行为的内在机制，挖掘使宏观特殊教育系统产生变化的原因以及宏观特殊教育系统形态产生变化后带来的影响，并通过计算机仿真，对宏观特殊教育系统进行跟踪或预测，从而对制定宏观特殊教育系统的发展战略提供参考。
3.1 宏观特殊教育系统的因果反馈图
从以上的分析可以看出，在构建系统动力模型中，尽管ct与dt、dt与et、et与at的拟合度一般，但其因果决定关系仍然是非常明显的，所以，宏观特殊教育系统的因果关系图可以表示为：
〔at〕→〔bt〕→〔ct〕→〔dt〕→〔et〕→
↑ │
┕┉┉┉┉┉┉┉┉┉┉┉┉┉┉┉┚
由于at与bt、bt与ct、ct与dt、dt与et、et与at之间都是正因果反馈关系，运用系统动力学的因果回路可以形象地表示为：
3.2 宏观特殊教育系统的流图及仿真
因果关系图只是构造了模型的框架，并没有区别不同性质的变量[4]。比如：状态变量的积累概念，因果关系中对积累效应与影响它的速率就没有加以区分。同时，因果反馈中为了简便，忽略了信息反馈链与物质流的差别，而用相同的实线箭头表示两种完全不同的概念。为了更加清楚地描述系统的构造，SD建模过程中用“流”的概念，采用特殊的符号构筑流图模型。在本例中，由于并没有涉及到流速等概念，只有积累，而且也并没有出现信息流，所以也不能体现出信息流与物流的区别，只是积累之间的效应，与因果关系图的区别不大，这里省略。
系统仿真是指利用计算机来运行仿真模型，模仿实际系统的运行状态及其随时间变化的过程，并通过对仿真运行过程的观察和统计，得到被仿真系统的仿真输出参数和基本特性，以此来估计和推断实际系统的真实参数和真实性能[5]。
在做具体仿真之前，还需要引入构造方程式可以定量地描述系统的动态行为。首先是level方程，即状态方程，该系统的level方程式为五个，可以统一表示为level(现在)=level(过去)+DT(输入流速－输出流速)，即Y.K=Y.J+DT(X1.JK-X2.JK)，其中DT表示时间间隔。计算时，首先给定t0时刻的初试值Y0(即Y.J)和前一个DT间隔内的速率值X.JK，得到现时的Y.K；然后再前进一个DT，把现时K时刻作为J时刻，把现在的L时刻为新的K时刻，再重复计算。其次是rate方程。SD的决策函数没有固定的格式，经常采用一些基本的速率变化模式来描述动态过程，比如：指数增长模型、指数衰减模型等。由于本例中，并没有涉及，所以在具体应用中才能决定到底采用那种变换模型。
最后，利用DYNAMO语言，对系统的SD模型进行仿真，对于不同的方案，仿真后进行比较，制定出当前最为有效的行动策略。
4 构建宏观特殊教育系统SD模型中存在的问题及构建的意义
4.1 存在的问题
4.1.1 20世纪90年代的特殊教育与21世纪的特殊教育的发展存在较大的差异
以现有的20世纪90年代后期的5组数据分析，随着时间的推移，人均GDP的增长，生均教育经费的增长，特殊学校的专任教师数和在校学生数以及毕业生数都是递增的。但是到了2001年以后，特殊学校的专任教师数首先开始减少，从2000年的3.2万人下降到了2.85万人，之后又开始在此基础上上升，2002年和2003年分别是2.98万和3.0万；在校学生数的变化比专任教师数迟滞了一年，趋势也不同，2001年是38.64万，2002年下降到37.75万，2003年又下降为36.47万；毕业生的变化也是从2002年开始下降，从2001年的4.63万下降到2002年的4.42万，到2003年又上升到4.5万。整体变化没有什么明显的规律性，从分布图上看，2000年以后，特殊教育的发展有一个缓冲的阶段，这种缓冲可以假设为我国残疾人口每年增加的绝对数量是不断减少的，但目前还没有确切的数据可以支持这种假设。