|
比例和比例分配都要用到率。率的这种意义至今仍然使用。刘徽拓展了率的意义,提出“凡数相与者谓之率”。成率关系的数量同时扩大或缩小同样的倍数,其率关系不变。比如甲、乙、丙三物有关系:甲:乙=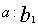 ,乙:丙= ,乙:丙=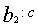 ,已知甲为A,问化成丙为多少?《九章》两次应用今有术,甲化成乙 ,已知甲为A,问化成丙为多少?《九章》两次应用今有术,甲化成乙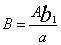 ,乙B化成丙 ,乙B化成丙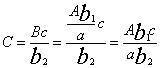 ,叫重今有术。刘徽认为,可以先把两个率关系中乙的率变成相同的值 ,叫重今有术。刘徽认为,可以先把两个率关系中乙的率变成相同的值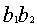 ,为了保持率关系不变,则甲的率须变成 ,为了保持率关系不变,则甲的率须变成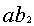 ,丙的率须变成 ,丙的率须变成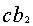 ,称为与乙相齐,即甲:乙:丙= ,称为与乙相齐,即甲:乙:丙=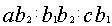 ,对甲、丙直接应用今有术: ,对甲、丙直接应用今有术: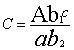 。刘徽把这种变换称为齐同原理。它源于分数通分,将a/b与c/d通分,化成相同分母:bd,然后使两者的分子与分母相齐,分别变成ad、bc,两分数变成ad/bd、bc/bd,这叫做齐其子,同其母。实际上,刘徽把分子、分母看作一组率的关系,与现代算术教科书关于分数的定义一致。 。刘徽把这种变换称为齐同原理。它源于分数通分,将a/b与c/d通分,化成相同分母:bd,然后使两者的分子与分母相齐,分别变成ad、bc,两分数变成ad/bd、bc/bd,这叫做齐其子,同其母。实际上,刘徽把分子、分母看作一组率的关系,与现代算术教科书关于分数的定义一致。
齐同原理在运算中作用特别大,而齐同方式则是多样的。如《九章》均输章题目:野鸭从南海飞至北海需7天,大雁从北海飞至南海需9天,若两者从南、北海同时起飞,问几天相逢?刘徽提出了两种齐同方式:飞一个单程,野鸭7天,大雁9天。若使两者天数相同,都是63天,则野鸭飞9个单程,大雁飞7个单程,与63天相齐。野鸭与大雁同时起飞,则63天飞(9+7)个单程,因此63/9+7天飞一个单程,即相逢日。齐同原理也可这样应用:一天野鸭飞单程的1/7,大雁飞1/9。若将一个单程分成63份,则野鸭一天飞一个单程的9/63,大雁飞7/63,一天共飞一个单程的9+7/63份,因此共飞一个单程需1÷9+7/63两者殊途同归,都证明了《九章》解法的正确性。
率与齐同原理,在其他运算中的应用,后面将陆续谈到。刘徽把它们看成运算的纲纪。
|