《九章》勾股章提出了若干已知勾股形三边中二者的和差等因素,求其边长的例题。赵爽、刘徽、贾宪先后作了进一步的发展,提出了一般性的公式及其证明。
国内外流行的印度莲花问题实际上是《九章》“引葭赴岸”题的改写。此题是:有一水池,方1丈,一株葭[jia佳,初生的芦苇]生在中央,高出水面1尺,引葭赴岸,恰恰与岸边相齐。问水深、葭长各多少?如图15,刘徽指出,水池边长的一半为勾a,水深为股b,葭长为弦c,葭高于水面者是弦股差c-b,这是已知勾与弦股差,求股、弦的问题:
图15 引葭赴岸 图16 竹高折地
1989年语文高考试卷有一古文今译题便采自《九章》勾股章“竹高折地”问:今有一株竹高1丈,被折断,末梢抵地,抵地处距竹根3尺,问剩余高多少?如图16,刘徽指出,抵地处至竹根距离是勾a,剩余的高是股b,折断部分是弦c,则竹高就是股弦和c+b,此是已知勾与股弦和,求股的问题: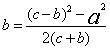
这两类题目互相返覆,刘徽以出入相补原理证明之。
有一门户,高比宽多6尺8寸,两角相距1丈。问此门户高、宽各多少?刘徽认为,将户宽作为勾a,高为股b,两角相距为弦c,那么这是一个已知弦c与股勾差b-a,求勾、股的问题。《九章》的解法经刘徽改写成
刘徽的出入相补证明方法是:以勾股和b+a为边长作正方形,称为大方,面积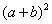 ;在其内部作一中方,其顶点在大方每边a、b的分点上,其边长自然为c,面积c2[c平方];在中方内部作四个以a、b、c为边长的勾股形,每一个面积为1/2ab,称为朱幂。中方除去四个勾股形,余一个以b-a为边长的正方形,称为黄方,面积为
;在其内部作一中方,其顶点在大方每边a、b的分点上,其边长自然为c,面积c2[c平方];在中方内部作四个以a、b、c为边长的勾股形,每一个面积为1/2ab,称为朱幂。中方除去四个勾股形,余一个以b-a为边长的正方形,称为黄方,面积为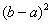 ,如图17,大方有八个朱幂,一个黄幂,中方有四个朱幂,一个黄幂,因此,中方减去半个黄幂等于半个大方:
,如图17,大方有八个朱幂,一个黄幂,中方有四个朱幂,一个黄幂,因此,中方减去半个黄幂等于半个大方: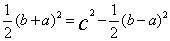 ,
,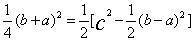 ,于是
,于是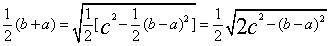 ,而由
,而由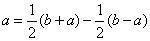 ,
, 证明了上述公式。
证明了上述公式。
图17 已知弦与股勾差求勾股的证明
有一门户不知高、宽,有人持一竹竿,不知长短,横着出门,长了4尺,竖着出门,长了2尺,斜着恰好能出门。问门的高、宽、斜各多少?刘徽把门户的高、宽、斜分别作为勾、股、弦,此题是已知弦勾差c-a、弦股差c-b,求勾、股、弦的问题。《九章》给出的公式是: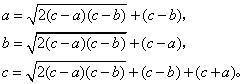
图18 已知弦勾差弦股差求勾股弦的证明
为了证明这些公式,刘徽首先指出了在弦幂中勾幂与股幂的相互位置,或矩于表,或方于里:若股幂为方形,则勾幂作为勾矩居于股方之表,如图18(1);反之亦然,如图18(2)。刘徽将其中一个图形旋转180°,与另一个重合,则成为图18(3)的情形。勾矩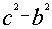 与股矩
与股矩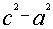 的面积之和应为弦幂c2。在图中,这两者在两角重合于两个以c-b为宽、c-a为长的长方形,其面积为2(c-a)(c-b)。而弦幂中却有一个以a+b-c为边长的小黄方未被勾矩与股矩填满。显然,小黄方的面积
的面积之和应为弦幂c2。在图中,这两者在两角重合于两个以c-b为宽、c-a为长的长方形,其面积为2(c-a)(c-b)。而弦幂中却有一个以a+b-c为边长的小黄方未被勾矩与股矩填满。显然,小黄方的面积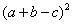 应等于2(c-a)(c-b),开方由
应等于2(c-a)(c-b),开方由
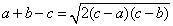
a=(a+b-c)+(c-b),
b=(a+b-c)+(c-a),
c=(a+b-c)+(c-b)+(c-a)
便证明了上述三式。
北宋贾宪把《九章》解勾股形的四个类型的方法抽象成一般性公式。杨辉又进而总结出a、b、c、c±a、c±b、b±a、a+b±c、c±(b-a)13种关系及变成b-a、c-b、a+b-c的段数,称作“勾股生变十三名图”。这13种关系包括了勾股形中勾、股、弦及其和、差的全部可能的关系,对勾股理论起着提纲挈领的作用。