|
旁要是先秦“九数”之一,西汉张苍、耿寿昌补充了解勾股形等内容后改称勾股,成为《九章》勾股章。根据贾宪、杨辉的提示,上述勾股容方、容圆及八个测望问题是旁要的内容。现在介绍这类测望问题。有一正方形城邑,不知大小,城门都在城墙正中。出北门20步有一株树。出南门14步拐向正西1775步,恰能看到此树。问城邑每边长多少?设城邑边长x,出北门a1,出南门k,折西b,如图21(1),考虑两个相似勾股形,小勾股形股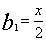 ,大勾股形勾 ,大勾股形勾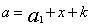 。由于 。由于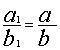 ,或 ,或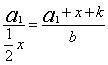 ,故 ,故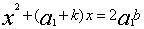 。这是刘徽推导此公式的第一种方法。第二种方法是:如图21(2),宽为DF=x,长为BC=x+a1+k的长方形DEGF,其面积x(x+a1+k),再考虑宽BC=x+a1+k,长为AC=b的长方形BCAI,它被对角线平分,由于勾股形AA1J与AA1G相等,故BC1JI与BCGF面积相等。DEGF的面积是BCGF的两倍,即BC1JI的两倍,BC1JI的面积为a1b,故x(x+a1+k)=2a1b。 。这是刘徽推导此公式的第一种方法。第二种方法是:如图21(2),宽为DF=x,长为BC=x+a1+k的长方形DEGF,其面积x(x+a1+k),再考虑宽BC=x+a1+k,长为AC=b的长方形BCAI,它被对角线平分,由于勾股形AA1J与AA1G相等,故BC1JI与BCGF面积相等。DEGF的面积是BCGF的两倍,即BC1JI的两倍,BC1JI的面积为a1b,故x(x+a1+k)=2a1b。
图21 出邑南北门
第二种方法的关键是长方形BC1JI与BCGF面积相等,它们有公共部分BC1A1F,则长方形FA1JI与C1CGA1面积相等。这是一个重要原理,后来贾宪、杨辉将其概括为:将一长方形斜解为二勾股形,两勾股形所容的以公共弦上任一点为公共点的两长方形的面积相等,见图22。这一原理在测望问题的出入相补中作用特别大。《九章》立四表望远、因木望山及测井径问题,都可以这样解决。如因木望山问是:有一树高9丈5尺,距山53里,人目高7尺。距树3里处望山,人目、树顶、山顶成一直线。问山高多少?如图23。由上述原理,阴影部分相等,故ab1=a1b,故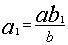 。 。
图22 容横容直原理
图23 因木望山
|