《周髀》载陈子应用勾股定理测望太阳距离时要开平方,但无开方程序。《九章》少广章提出了世界上最早的开平方的完整抽象程序。刘徽认为,开平方的几何意义是已知一正方形面积求其边长。《九章》按四行布算,最上行准备放议得(即根),下面一行布置被开方数,称为实,第三行是法,最下一行是借一算,与实的个位相齐,这相当于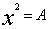 ,如(1)。将借算自右向左隔一位移一步,至不能移为止。根的位数比移的步数多1,实是个位、十位数,借一算根是一位数,实是三位、四位数,借算移一步,根是二位数,依此类推,如(2)。议所得(根的第一位)
,如(1)。将借算自右向左隔一位移一步,至不能移为止。根的位数比移的步数多1,实是个位、十位数,借一算根是一位数,实是三位、四位数,借算移一步,根是二位数,依此类推,如(2)。议所得(根的第一位)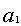 ,以
,以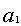 乘借算
乘借算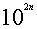 得
得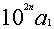 ,为法,应使A÷
,为法,应使A÷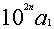 得到
得到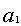 后余数小于
后余数小于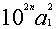 。刘徽认为这一步是以
。刘徽认为这一步是以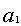 乘法
乘法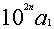 减A,即
减A,即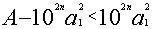 ,如(3)。其几何意义是从面积为A的正方形中减去以
,如(3)。其几何意义是从面积为A的正方形中减去以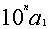 为边长的正方形黄甲,如图27。
为边长的正方形黄甲,如图27。
再求第二位得数。撤去借算,将法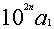 加倍,为定法,如(4)。刘徽认为其几何意义是与黄甲相连的两朱幂的长
加倍,为定法,如(4)。刘徽认为其几何意义是与黄甲相连的两朱幂的长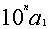 ,此朱幂的宽是第二位得数。将定法向右退一位,为
,此朱幂的宽是第二位得数。将定法向右退一位,为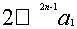 ,再在下行个位上布置借一算,自右向左隔一位移一步,显然只有n-1步,即
,再在下行个位上布置借一算,自右向左隔一位移一步,显然只有n-1步,即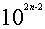 。求根的第二位得数相当于求减根方程
。求根的第二位得数相当于求减根方程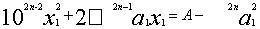 的正根,如(5)。议得
的正根,如(5)。议得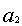 ,以
,以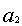 乘借算10(2n-2),加定法,得
乘借算10(2n-2),加定法,得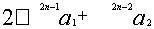 ,使得
,使得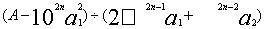 的商是
的商是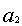 ,而其余数小于
,而其余数小于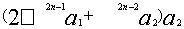 。刘徽认为这一步相当于求出余实
。刘徽认为这一步相当于求出余实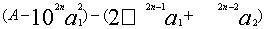 ,如(6)。其几何意义是从正方形余下部分中减去两朱幂及以
,如(6)。其几何意义是从正方形余下部分中减去两朱幂及以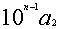 为边长的小正方形黄乙。若余实仍不为零,则继续开方。显然,这种方法对任何自然数的开方都是适用的。《九章》的例题中被开方数有的高达10位,如
为边长的小正方形黄乙。若余实仍不为零,则继续开方。显然,这种方法对任何自然数的开方都是适用的。《九章》的例题中被开方数有的高达10位,如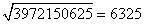 。如果被开方数是分数,则通分后,分子、分母分别开方,然后相除,如:
。如果被开方数是分数,则通分后,分子、分母分别开方,然后相除,如: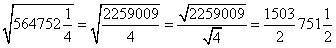
图27 开平方术示意
如果分母不可开(无理数),则以分母乘实,开方之后,除以分母: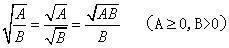
《九章》少广章说:“若开之不尽者为不可开,当以面命之。”这里“不可开”大体相当于无理数。《九章》之后,对开方不尽的情形,有人以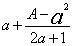 表示
表示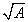 的近似值,刘徽指出,这个值太小,应有不等式
的近似值,刘徽指出,这个值太小,应有不等式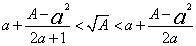 。刘徽又提出,为得到
。刘徽又提出,为得到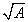 的精确近似值,求出整数部分之后,应继续开方,“求其微数”,以十进分数逼近
的精确近似值,求出整数部分之后,应继续开方,“求其微数”,以十进分数逼近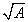 。他说:“退之弥下,其分弥细,则朱幂虽有所弃之数,不足言之也。”《九章算术·少广章注》)刘徽的思想不仅开十进小数之先河,而且是保证我国圆周率计算在世界上领先千余年的先决条件,此是后话。
。他说:“退之弥下,其分弥细,则朱幂虽有所弃之数,不足言之也。”《九章算术·少广章注》)刘徽的思想不仅开十进小数之先河,而且是保证我国圆周率计算在世界上领先千余年的先决条件,此是后话。
《孙子算经》、《张丘建算经》未提出抽象的开方程序,但从题目的开方细草中可以看出,它们在求得根的一位得数后,不再撤去借算,而是保留借算,改称下法,退二位求减根方程。它们还吸取了刘徽的改进。北宋贾宪提出立成释锁法,继承了以往开方法的长处并加以改进,与现今方法无异。
一次项系数不为零的开方称为带从开方。《九章》勾股章有需开带从平方的例题(见第五节),而未有开方程序。但是,上述开方程序中从求第二位得数起,便是开带从方。