草曰:立天元一为勾,地元一为股,人元一为弦。三才相配求得今式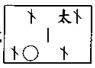 ,求得云式 ,求得云式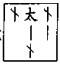 ,求得三元之式 ,求得三元之式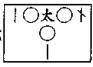 ,以云式剔而消之,二式皆人易天位,前得 ,以云式剔而消之,二式皆人易天位,前得 ,后得 ,后得 ,互隐通分,相消,左得 ,互隐通分,相消,左得 ,右得 ,右得 。 。
|
解:设x为勾a,y为股b,z为弦c,由已知条件列出x+y+z-xy(z-y)=0或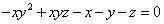 (今式)。 (今式)。
同样
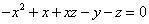 (云式)。 (云式)。
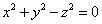 (三元式)。 (三元式)。
以云式减今式,以x除,并将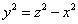 , ,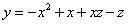 代入,便得到前式: 代入,便得到前式: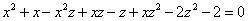
将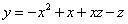 代入三元式,便得到后式: 代入三元式,便得到后式: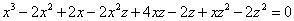
并将人元摆到天元上。互隐通分相消,得到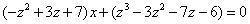
为左式,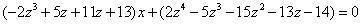
为右式。 |
(罗士琳细草:以前式左行齐之,得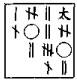 ,消前式,得 ,消前式,得 ,又以前式消之,得 ,又以前式消之,得 。复以前式左行齐之,得 。复以前式左行齐之,得 ,三因前式,得 ,三因前式,得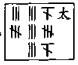 ,消之得 ,消之得 为左式。以左行齐前式得 为左式。以左行齐前式得 ;以以前式左行齐 ;以以前式左行齐
|
[以前式左行(-z+1)乘后式,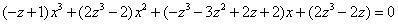
以x乘前式,得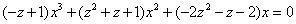
两者相消,得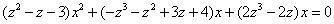
又以z乘前式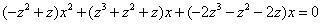
与之相消,得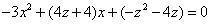
以前式左行(-z+1)乘此式,得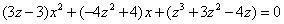
以3乘前式,得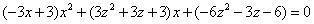
两者相消,得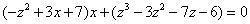 为左式。 为左式。
以左式x的系数乘前式,得到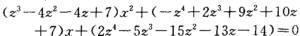
以前式x2的系数(-z+1)及x乘左式,得 |
左式,得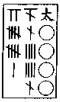 ,相消得 ,相消得 为右式。内二行得 为右式。内二行得 ,外二行得 ,外二行得 ,内外相消,四约之,得开方式 ,内外相消,四约之,得开方式 ,三乘方开之,得弦五步。 ,三乘方开之,得弦五步。
|
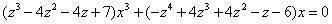 两者相消为右式: 两者相消为右式: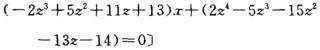
内二行相乘得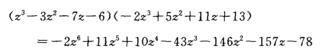
外二行相乘得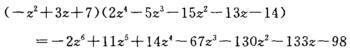
两者相减应为0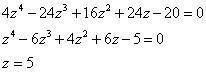 |