等差级数问题在宋元时代发展为高阶等差级数求和问题。这一课题的开创者是北宋大科学家沈括。沈括研究了《九章算术》的刍童等立体体积公式(见第四节),认为已相当完备,但是,没有求隙积的方法。隙积就是积之有隙者,如将一颗颗棋子、坛、罐等垒起来,如图34,虽然有刍童的形状,但因有刻缺空隙,若用刍童术求积,数值偏小。沈括便提出了隙积术。设隙积的上底宽a1,长b1,下底宽a2,长b2,高n层,且a2-a1-b2-b1=n-1,沈括提出的隙积术是: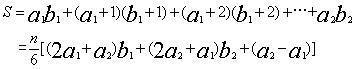
图34 隙积
即刍童状隙积中物件的个数比刍童体积多n/6×(a2-a1)。隙积术实际上是一个二阶等差级数求和问题:
|
级数 |
a1
b1(a1+1)(b1+1) |
(a1+2)(b1+2) |
(a1+3)(b1+3) |
(a1+4)(b1+4) … |
|
一阶差 |
a1+b1+1 |
a1+b1+3 |
a1+b1+5 |
a1+b1+7 … |
|
二阶差 |
2 |
2 |
2 |
2 … |
南宋杨辉《详解九章算法》以各种菓子垛比类《九章》的立体。其中刍童形菓子垛与沈括的隙积术相同。四隅垛(比类方锥、阳马)的求积公式为: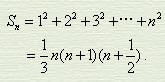
方垛(比类方亭)的求积公式为: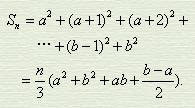
三角垛(比类鳖臑)的求积公式为: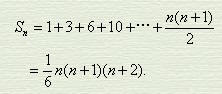
不难看出,这都是二阶等差级数求和问题。同时,可以看出,在沈括的隙积术中令
a1=b1=1,a2=b2=n,便是杨辉的四隅垛公式;令a1=b1,a2=b2,便是杨辉的方垛公式;令a1=1,b1=2,a2=n,b2=n+1,便成为两个三角垛之和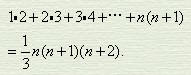
两端除以2,便得到杨辉的三角垛公式。