首页 -> 2007年第10期
让学生在探究问题中体验成功
作者:焦亚峰
(一)创设情境,激发兴趣
知识源于生活,首先以现实生活中学生喜闻乐见或感兴趣的实物原型为基点,从中引发问题,激发兴趣。同时,借助多媒体展示具体的轴对称现象和轴对称图形,例如蝴蝶、京剧脸谱等。通过欣赏,使学生认识到现实生活中存在许多轴对称图形,从而进一步引发对于轴对称的性质及应用认真探索和研究的兴趣。
(二)设疑探索
教学设计中的好问题,首先要是一个“初始问题”。所谓初始问题,就是那些可以导致数学知识(概念、定理、法则、方法甚至思想、观念)产生的问题。这里以课本原型作为初始问题的设定。
1.“课本原型”。
例1.如图1所示,要在街道旁修建一个奶站,向居民区A、B提供牛奶,奶站应建在什么地方,才能使从A、B到它的距离之和最短?
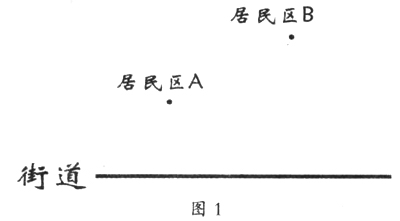
(1)此问题学生在初一已研究过,所以很快便口答出解题方案。即作A或B关于街道的对称点,连接对称点与另一个居民区,它与街道的交点P就是奶站的位置。
(2)教师继续设问:为什么建在此处距离之和最短?——引导学生明白道理,为本节课奠定理论基础。
2.“活学活用”。
变式1:如图2,菱形ABCD中,AB=2, ∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值是____。
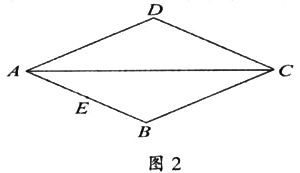
此问题一出示,学生的思维立即被调动起来,很快投入到积极的探索之中。但此问题从表面上截然不同于例1,所以许多学生一时很难找到解决途径。这时我适时地给予启发:①此问题能否转化为例1的问题?②菱形是轴对称图形吗?它的对称轴是什么?
学生在我的启发引导下,恍然大悟,很快将问题转化为例1的形式,得出解决方案。初战告捷,这时我看到大部分学生的脸上都露出成功的喜悦。
变式2:如图3,A为半圆上一个三等分点,圆弧AB等于圆弧BF,P是直径EF上一动点,⊙O的半径为1,则AP+BP的最小值是____。

学生在经历了例2的探索转化后,对于此例很快能找到解决方法,但此例的计算学生有些困难,部分学生又一次陷入困惑之中。这时我又给予适时地点拨,使这部分学生茅塞顿开。再战告捷,学生情绪高涨,兴趣大增。我趁机让他们总结出了“在直线上作一点,使得这一点到直线同侧两点的距离之和最小的方法”。
3.“挑战自我”。
变式3:如图4,P点处设有一垃圾站,OM、ON分别为两条道路,现想在两条路上分别设立两个垃圾桶,为了使垃圾车能先从垃圾站出发到OM上垃圾桶取垃圾,然后再到ON上的垃圾桶取垃圾,最后回到垃圾站的距离最短,问OM、ON上的垃圾桶应设在何处?
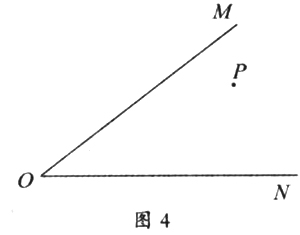
学生很快又投入到探索之中,但这道题与前三道题又截然不同。经历了一段艰难的探索之后,同学们终于找到了作图的理论根据,脸上露出满意的微笑。
4.“大展身手”。
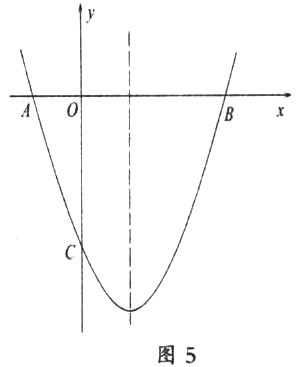
(2005海南省试验区)如图5,抛物线y=x2+bx+c与x轴交于A(-1,0)、B(3,0)两点。
(1)求该抛物线的解析式;
(2)设(1)中的抛物线交y轴于C点。在抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由。
此题是一道综合题,一方面考察二次函数解析式的确定问题,另一方面是对本节课所学知识的灵活应用。由于前面问题中学生积极探索,已获得了较高的分析问题和解决问题的能力,故此问题轻松得以解决。
本节课通过层层设计、环环相扣的问题,由浅入深,把学生带入一种不断探索和享受成功喜悦的状态当中,引人入胜。就像登山,虽经历了跋涉的艰辛,却欣赏到了无限美景,让人神清气爽,心旷神怡。这节课虽然结束了,但它留给我和学生的却很多很多……