首页 -> 2007年第10期
以问题的思考为切入点,培养学生数学交流能力
作者:王耀武
[课堂实录]
师:请大家观察黑板的四角,窗框的四角,知道它们的度数吗?
生:(齐答)900。
师:请你们动手量一量,它们的度数是否等于90?
(同学们纷纷操作起来)
师:是900吗?
生:是。
师:把黑板的一个角画出来,并把这个角的两边分别反向延长。
(学生在操作的同时,老师也将图画在黑板上)
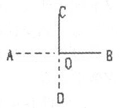
师:(指着图)像这样两直线相交所形成的四个角中有一个等于900,称为两直线互相垂直两直线的交点叫垂足,垂直用符号“⊥”表示。(板书课题——垂直)
[解读]教师从学生身边熟悉的黑板、窗框入手,把学生带入一个思考的情景,激活了学生基本的数学语言及方法。黑板、窗框在教学中的运用,把抽象的“垂直”概念具体化,起到了直观教学的作用,达到了让学生对抽象概念深刻理解的教学目标,同时利用师生对话,促使学生抽象垂直模型的形成,增加了学生内存数学语言。
[课堂实录]
师:请大家在方格纸上画出垂直的两条直线。
(两位同学走上讲台在黑板上画,其余在下面迅速行动起来)
(没多大工夫,部分同学便表现出成竹在胸的神态,讲台上的两位同学也很快完成了)主要有以下三种情况:

学生甲:我画出来的是第一种图形。
学生乙:我把三种图形都画出来了。
师:后面两个图形中的两条直线垂直吗?
学生乙:我用量角器量得∠ACB、∠ABC都是等于900,所以它们垂直。
师:能用学过的探究方法画出这些垂直的直线,做得不错。
学生丙:横行5个,竖行5个正方形方格,同样画出的直线也是垂直的,更多的正方形方格画出的直线也垂直。
[解读]设计这个画图环节,意在让学生通过动手操作,利用学过的探究方法,在所给的情景中,从不同的角度正确画出已经建立起来的垂直模型。通过展现自己的成功之作,激发学生的表达欲望,在对话与交流过程中引导学生反思,拓展学生思维面,逐步渗透逻辑分析与判断思维,发展学生数学交流语言。
[课堂实录]
师:请大家拿出一张长方形纸,随意翻折,能折出多少种垂直的折痕?
(大约过了2分钟,同学间便讨论起来)主要出现以下几种情况:
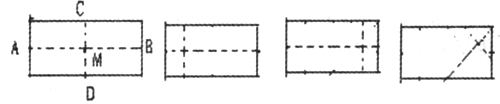
师:大家在下面折得很好,能说说怎么判断这些折痕垂直?
学生A:用量角器量得其中一个角是900,所以它们垂直。
学生B:第一个图因为是对折得到的两条折痕,所以∠CMB=∠DMB。又因为∠CMB与∠DMB组成一个平角,即∠CMB+∠DMB=1800,这样可以知道∠CMB=900。所以,AB⊥CD。
师:这位同学善于观察与思考,能结合学过的知识来分析判断,说得很好。
学生C:我还有另外的折法……
[解读]折纸活动的开展,让学生把从生活中抽象出来的几何模型又放回实际生活中,在生活中感受这种趣味模型,创造这种特殊美丽的模型。在体验与创造的过程中引发思考,催生新的数学语言。
[课堂实录]
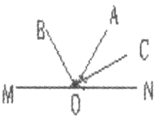
师:请看问题,如图,点O是直线MN上的任意一点,OA为一条射线,OB平分∠MOA,OC平分∠NOA。问:OB与OC垂直吗?为什么?
(教室内一片寂静,同学们进入探究状态,过了3分钟,同学们便讨论起来)下课铃响了。
[解读]本题的设计从一定的深度来引导学生对垂直模型进行探究,对七年级学生来说,具有较大的探究价值。学生通过独立思考,把已有的知识和探究方法激活,逐渐生成新的知识及方法。在这个过程中,增加学生内存数学语言,提高基本技能。通过生生交流,师生交流,促使内存数学语言数量的继续增加,语言质量的提高;促使技能的成熟与发展,强化逻辑分析与判断,渗透逻辑推理。
(二)反思与体会
《新课标》指出,合作交流是学习数学的重要方式。如何培养学生的数学交流能力?建构主义学习观认为,学习是认知框架的不断变革与重组,问题是建构的起点。案例以问题的思考为切入点,创设不同形式的问题情景,充分激发学生的好奇心、成功感,把学生带入操作与思考的课堂,逐步培养学生的数学交流能力。
1.创设学生熟悉的问题情景,激发交流欲望。数学来源于生活,又服务于生活。本节课以教室内学生常见的黑板、窗框为问题背景,学生倍感亲切,轻松自然地进入思维状态,将这些固定的生活材料演化为自身的数学语言成分,产生沟通、对接与印证的愿望,通过师生交流互动,增加内存数学语言,促使完美垂直模型的形成。从生活中数学知识入手,学生易感知,思维灵敏,数学语言得以迅速发展。
2.创设成功问题情景,激发交流情感。在正方形方格纸上画垂直的两条直线,这实际上是将已形成的抽象几何模型建立在一个新的环境中,是知识的迁移与运用。这个过程学生容易完成,但对七年级学生来说,不容易把所有的情况都画出来。本题是一道开放性试题,学生能比较轻松地画出一种垂直情况,产生浓浓的成功感与展示意愿,对话与交流已是水到渠成。通过对话与交流的进行,学生又回到理性状态:原来可以画出这么多种垂直情况!从而进一步激发学生的学习思考。
折纸是一项有趣的活动。《新课标》指出,动手实践是学习数学的重要方式。折纸活动的开展,让学生把从生活材料中抽象出来的垂直模型又放回生活实际中,利用生活材料创造这种美丽的图形,感受这种创造的成功,在积极的交流与对话过程中,拓展思考渠道,逐步丰富学生的内存数学语言。
3.创设有探究价值的问题,促使理性交流。最后一题对七年级学生来说,综合性强,有一定的探究价值。通过学生自主探究,激活已有知识及方法,逐渐建构新的知识框架及方法,增加学生数学语言的内存数量及质量,达到“心求通却未得,口欲言却不能”的更高境界。学生的自发讨论便说明这一点。探究会促使交流更具理性,广泛的数学交流又促进学生认知建构的成熟与发展,不断提高交流水平。
与此同时,困扰数学课堂广泛交流的因素,如学生之间的差异性过大,不利于数学交流活动的广泛深入进行;交流多停留于中上等层次学生,基础差的学生难以有效地参与进来;参与面不广,交流效率不高等,值得进一步思考。