首页 -> 2008年第1期
“分类”在数学教学中的妙用
作者:张再良
学生在入学前已有一定的关于分类问题的生活体验。据测验,六岁以后的儿童能进行一级概念独立分类的人数超过一半,9岁时可达90.6%。因此,在小学数学教学中可进行分类思维方法的训练的题目很多。例如在一年级就有:①给同类图形涂上相同的颜色。
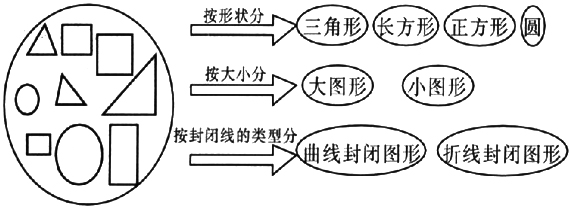
②给三种颜色的三个三角形和两种颜色的三个正方形分类
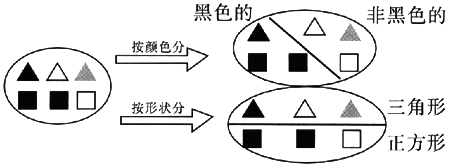
例①②都是按照某一种特性进行分类,称单因素特征分类。单因素特征分类可以帮助我们把知识系统化、条理化,把一个复杂的问题按规定场合要求,提出所提供的材料中与问题有关或无关的因素,发现带有规律的特征,从而提高处理复杂问题的能力和学习效率。从以上两例还可以看出,按不同的分类标准有不同的分法。所以我们在教学这些问题时,应充分发挥学生的观察、想象与判断能力,发展学生的创造性思维。只要学生能正确地说出分类标准都是可以的。
分类是一种重要的思维方式,我们在教学中应具有分类的意识,恰当有机地运用分类,引导并教会学生对数学知识进行分类,理清知识结构,提高教学效率。
(一)利用分类,揭示课题
课堂教学的开始部分,对知识进行分类,可有目的选择教学内容进行教学。例如15个小石子,按要求分,刚好分完吗? 将分的结果填在方框里。
每份()个,共有()份,( )15÷□=□
每份()个,共有()份,( )15÷□=□
每份()个,共有()份,( )15÷□=□
每份()个,共有()份,( )15÷□=□
每份()个,共有()份,( )15÷□=□
组织学生讨论,把分的结果分成两类:

小结揭题:用除法计算平均分时,往往有两种结果,一种刚好分完,一种分后还有剩余。我们把分后还有剩余的那个数叫余数,今天我们就来学习“有余数的除法”。
(二)逐级分类,理清内涵
有些概念由多个要素组成,学生学习判断时往往会顾此失彼。利用逐级分类,步步深入,揭示概念的内涵。例如方程的概念有两个要素:一是等式、二是含有未知数。注意点是理解未知数的外延。教学是先出示8个式子后提示:x、a、b等都称未知数。
X-7=0 9x-4 15÷X=1 18+2a<100
8+7=15 12x=84 9-x>4 76-18×2=40
你能给上述8式进行分类吗?
第一层是先按是否是等式分:
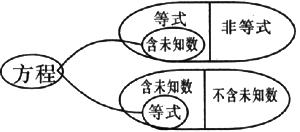
或是先按是否含有未知数分:
第二层是再给等式分类,或给含有未知数的式子分类。
最后抽象概括:含有未知数的等式是方程。
(三)巧用分类,探究规律
有些教学内容,如果在教学过程中设计分类环节,可有效突出要点,引起对分类结果的探索。例如教学商不变的性质,可设计以下一组试题,要求学生区分商变化与商不变两类。
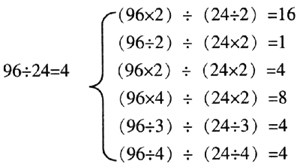
先将这六个除式分别归为两类:
商变化 商不变
(96×2)÷(24÷2)=16 (96×2)÷(24×2)=4
(96÷2)÷(24×2)=1 (96÷3)÷(24÷3)=4
(96×4)÷(24×2)=8 (96÷4)÷(24÷4)=4
然后引导学生寻求商不变的规律,这样教学,学生从分类中强化商不变的性质。
(四)运用分类,梳理知识
学完某一个单元或某一阶段后,教师可将这些内容按不同的分类方法进行知识的归类,使知识系统化、条理化,有助于知识的巩固。例如:
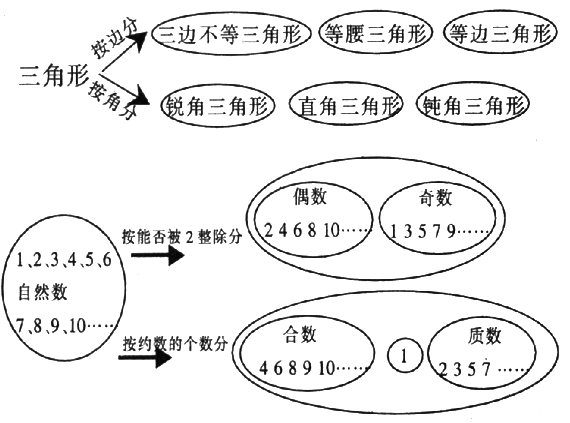
分类是一种应用很频繁的思维方式,我们要善于利用分类,提高数学课堂教学效率,帮助学生减轻课业负担,做到既轻松掌握数学知识,又扎实发展数学思维。