首页 -> 2008年第3期
让数学游戏走进数学课堂
作者:陈建金
[关键词]数学游戏 数学课堂
数学游戏以其优雅、趣味的形式“娱人”,以其丰富、新颖的内容“引人”,以其巧妙的解法、无穷的魅力“迷人”,以其潜在的功能“育人”。长期的数学教育理论和实践都已经证明游戏对于数学学习有极大的价值。经常做数学游戏,不但使学生变得更聪明,而且还会喜欢上数学。正如苏霍姆林斯基所说:“世界通过游戏展现在孩子面前,人的创造才能常常在游戏中表现出来,没有游戏也就没有充分的智力发展。”
本人结合理论学习和教学实践,针对新版教材的特点,尝试从以下几个方面将游戏引入课堂教学,让学生在轻松愉悦的氛围中得到知识的提升,在情趣盎然的学习过程中得到能力的发展。
(一)通过数学游戏加深学生对数学概念的理解
数学概念教学是数学教学的重要组成部分,因为数学概念是进行推理和判断的基础,清晰的概念是进行正确思维的前提,但也是教学的难点。因此,在新概念教学中引入教学游戏,不失为一种好方法。
如在教学无理数概念时,用掷骰子来引入无理数概念。在课堂上问学生骰子有什么作用,当学生纷纷回答骰子用于搓麻将时,告诉学生骰子还有一种新的用处,而且与数学有关——可以用来产生一种新的数。然后请两位学生上讲台前来,一位学生在讲台上掷骰子,另一位学生在“0”小数点后面写上骰子掷出的点数,随着骰子一次次地掷,黑板上出现了不断延伸的小数,0.136245135……我喊了“暂停”,然后通过恰当的提问,从而引出无理数的概念,这样的教学设计,使学生接受“无理数”这一难懂的概念时,因为有了游戏的铺垫,而变得较为亲切。
(二)通过数学游戏丰富学生对平面图形的认识与感受
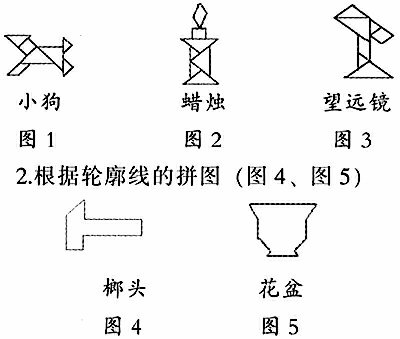
在教材七年级上册第四章安排了“有趣的七巧板”一节。七巧板是我国古代人民创造的益智游戏,被称为“东方魔板”。虽然它只有非常简单的七块,但同它拼出的图形成千上万,诸如建筑物、器物、人物、鸟鱼虫兽等等,千姿百态、惟妙惟肖、令人叫绝。根据教材编排设计一堂兴趣课,带领学生开展这一活动。游戏过程设计按以下三个层次逐步上升。
1.按所提供的图象(图1、图2、图3)进行拼搭。
3.自由拼图,根据自己想象出来的物体的形象,把它拼出来。以下是学生拼摆的图形(图6—8)
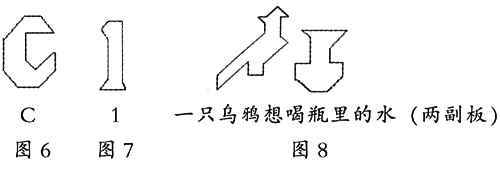
学生通过对七巧板的拼拼摆摆,不但能引起学生对几何图形的兴趣,而且进一步丰富了对平行、垂直及角等有关知识的认识。
又如在八年级上册第四章安排了“平面图形的密铺”一节。在学习书本知识后,可设计一个游戏,也很有意思。游戏过程设计分两个步骤:①学生分组合作,制作一些多边形卡片,通过动手拼摆,能否用其中的一种或多种拼搭成一个平面图形。②学生把一个任意四边形剪成四块,动手拼图,探索能否拼成别的图形,并从中体会图形的变换(图9—12)。

通过这些游戏,加深了学生对平面图形的认识,丰富了学生的想象力,感受了数学美,激发了学生的发散思维和创新意识,并且通过小组合作,培养了学生团结协作的精神和良好的个性品质。
(三)通过数学游戏发展学生的空间观念
初中生抽象及空间想象能力相对较弱,所以在讲授某些空间图形时,教师要设计好教学,努力使抽象的内容具体化、形象化。八年级上册第一章“蚂蚁怎样走最近”这节课,要由立体图形想象出它的平面展开图,内容抽象,学生较难掌握。因此,在上课时,首先,组织学生进行折纸游戏,通过剪一剪、折一折引导学生探索立体图形与平面图形的关系,为后面的例题教学做好铺垫。再次,出示教材例题,“有一个圆柱体,它的高等于12厘米,底面半径等于3厘米,在圆柱下底面的A处有一只蚂蚁,它想吃到上底面与A处相对的B处的食物,沿圆柱体侧面爬行的最短路程是多少?”(如图13所示)
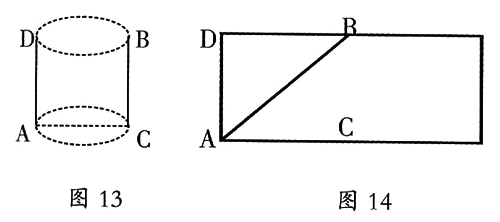
学生通过讨论得出两种不同的结论,一种认为最短路程是Rt△ACB斜边AB的长,另一种认为是把圆柱体的侧面沿AD展开成为一个矩形,Rt△ADB的斜边是最短路程。可引导学生把两种方法都试一试,比较两者的不同。由于前面学生做了折纸游戏,已经对立体图形和平面图形的关系有了一定的认识,所以,很快地第一种想法的学生认识到自己的错误所在,并寻求出正确答案(如图14)。
又如新教材的同步练习册对三棱锥的三视图给出了两种不同的答案,学生有疑问,可不正面回答,而对学生说:“动手操作,做游戏会得出解释的。”学生通过对三棱锥不同摆放位置的观察,讨论后作出正确的解释:三棱锥的三视图会随着摆放位置的不同而呈现出多种情况,其它立体图形亦然。
(四)通过数学游戏丰富学生对概率的认识,发展学生的统计观念
统计与概率是初中数学教学的重要内容之一。北师大新版教材在这部分教学内容的编排中安排了许多游戏。如通过“抛硬币”、“转转盘”、“摸有色小球”等游戏来加深对概率的认识,通过“掷骰子”来感受事件的可能或是确定,通过“抢20的游戏“来体验机会的均等或是不平等。在“数据的收集与处理”等几章中更是要鼓励学生走出课堂,通过收集、处理数据,体会数据在解决现实问题中的重要作用。
如八年级下册第五章第二节“数据的收集”的教学,组织学生选“新班长”,并提出两个要求:①公正、公开、公平的选举;②“新班长必须是大多数同学能接受的。学生们设计了多种选举方案,通过讨论一致认为采用“投票推荐”的方法最符合要求。活动结束后,学生们都有点惊讶,选“新班长”也是数学吗?在统计与概率知识的教学中,常常做上述的游戏的同时,“频数”、“频率”、“概率”、“可能”、“不可能”、“必然”等词语也自然成为学生的口头禅。
(五)通过数学游戏让学生体验数形结合思想
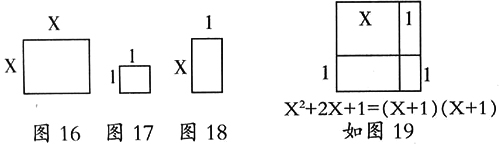
如教学二次三项式的因式分解,首先让学生拼凑许多边长为X和1的正方形与长和宽各为X和1的长方形的板片(如图16、 图17、 图18)以便获得相应的感性知识。接着要求学生用这些板片拼成一个比‘X·X正方形’更大的正方形,学生稍加尝试便完成拼凑。而后要求学生描述自己所做的工作。学生进行观察、思考、讨论,教师根据情况予以提示和提问,大多数学生都会说:这个正方形是一个‘X·X正方形’和两个‘1·X’长方形加上一个‘1·1正方形’拼成的。教师引导学生用标记法记下‘X·X正方形’用X2,加用‘+’表示。在讨论中学生还可能从边的角度来表示,即(X+1)(X+1),由于两者都表示同一个正方形面积,所以就有等式X2+2X+1=(X+1)(X+1),至此,二次三项式的一种因式分解模式就被“发现”了(如图19)。
(六)通过数学游戏激发学生对数学竞赛辅导的兴趣,提高辅导效果
教师在数学竞赛辅导时适当引入游戏,让学生进行所谓的“胡思乱想”,不失为一种好方法。如在一次竞赛辅导中,表演猜扑克牌的游戏,拿出一副52张不含王牌的牌,让随便哪位学生任意抽取5张,交给另一位同学,另一位同学将其中的4张牌一字排开,依次亮在桌上,然后笔者猜出没有看到的那一张牌的花色和牌点。如此猜了六、七次,全部正确,这无疑引起了学生的强烈好奇心。笔者了个关子说:“这是一种巧妙运用数学知识的扑克游戏,你能知道其中的奥秘吗?学生讨论后,再娓娓道来。显然学生的学习兴趣浓厚,辅导效果好。
新教材为了更有利于学生技能的训练和能力的提高而设置了很多学生游戏素材,这些游戏“题内有话、话外有话”,老师应该更多地携“数学游戏”进入课堂。皮亚杰认为“智慧自游戏发端,活动是连接主客体的桥梁”。“做一做”能使学生获得一种新的知识、新技能,“玩一玩”会开启学生智慧的大门,提高解题能力。当然,游戏的方法不能代替一切,数学游戏不能单纯地停留在“好玩”上,教师必须在游戏中引导学生通过亲身参与和独立探索,构建自己的数学知识,获得对数学的理解,拓宽解题思路,使数学真正起到磨练思维的作用,让学生正切体验到学习数学的快乐。