首页 -> 2008年第3期
在数学练习中落实“过程与方法”目标的思考
作者:余爱军
学期初的一次数学练习,布置了这样一道题目:
有三种不同长度的小棒,你能摆出几种不同形状的长方体框架?
_________4cm 6根
____________5cm 8根
_______________6cm9根
学生第一次作业十分不理想,存在许多问题:
1.钻题目空子,学生根本不去思考。许多学生作业中这样作答:“我能摆出1种”、“我能摆出2种”。这样的回答其实学生的思考性几乎为0。作业访谈中一个学生坦言:“老师,这种题目既然说有几种不同的方法,那肯定有1种以上的方法的,又没要求非得写出全部。我想都不用想就答有1办法了。”
2.没有合理的过程展现,学生思考深度不深。上述这样表达的学生中,也有部分是在思考之后作出回答,但结论显示出他们的思考深度是欠深的。学生大部分只是直觉应该各选4根。对于这里的8根、9根两种材料信息根本没有去思考多选的可能性。当然两面是正方形的情况也就根本不能发现。其实这种长方体的特征在新课探索中学生都有发现。为什么学生在实际问题中就联想不到?
3.结果表达不完整,思考过程混乱。在具体每种选择分类记录的学生中,大部分学生在记录方式上暴露出记录的随意与方法的无序。许多学生记录“我选4cm长的4根,5cm长的4根,6cm长的4根。”或者就在原题三根线段边上记一下“4根”。
4.思考记录方法不多、不善用、不会用,影响了问题解决质量。其实诸如此类多可能性的问题解决采用列表记录、分类整理记录等,这样的思考过程与方法在新知探索阶段的课堂上是展现过的,学生应该有经验基础,但当学生独立思考问题时,却用不出来。
根据这些问题,笔者便安排时间让学生再次集中做一做。并明确要求:写出所有的情况。
(二)交流过程剪辑
师:你是怎样选的?
生1:4cm4根,5cm4根,6cm4根。
(教师随即利用题目内容绘制了一张记录表)

师:为什么这样选?
生:长方体有12条棱,4根一样长,4根一样长……
师:那这样的长方体接近下面的哪个图,为什么?

生:正方体,因为这个长方体的长、宽、高很接近的。
师:感觉真不错,找到了数量间的关系。还有不同的摆法吗?
生:4cm4根,5cm8根。
师:这样选的长方体有什么特点?
生:有两个面是正方形的。
(生的思路忽然被击荡开了)
生:还可以是4cm4根,6cm8根。
生:也可以是5cm4根,6cm8根。
………(五种方法纷纷展现。)
师:刚才我发现有的同学思考记录很有方法,有的像老师一样用表格,保证清楚又准确,也有同学用符号:A、(1)4根 (2)4根(3)4根;B、(1)____4根 (2)______8根 (教师随机展示了学生中几种不同的思考记录过程。)
师:这些记录方法清晰,又反映了思考过程,是数学学习思考能力的一种表现,我们在分析思考时要会用各种简单的符号记录思考过程,做到有序清晰的思考……
(三)思考
“过程与方法”是三维目标之一,也是教学学习务必高度关注和追求的目标。平日应更多地从新知的探究中去发掘“过程与方法”时机,把目标达成融化在新知探索中。这也逐步成为对“过程与方法”目标认识及落实的一种惯性思维。但数学新课探索交流阶段让学生有了方法与思考过程的初浅体验,可是学生个人对这些方法与策略的认知建构是不到位的。上述案例中,学生在独立练习时出现方法运用力不从心现象。主要原因是课堂探索阶段看似形成了多种方法,老师也进行了当场展示,但这更多的是学生的集体(群体化)的方法,并未让每个学生真正理解或掌握。
练习中是不是可以强化这种过程性功能?练习是不是也应该起促进过程与方法目标达成的作用?在本案例的尝试中,笔者认为数学教学应该挖掘出“练习”中的方法价值。因为练习不只是一种单一巩固与训练基础知识技能的活动。
1.练习是学生新课后真正独立的学习时间,是学生数学知识与学习方法真正掌握与提升的过程。新课中对方法掌握的程度如何?在独立练习中就可以“牛刀初试见分晓”,这也符合学习认知心理规律。为此,练习不是方法目标落实的盲区,而是“亮点”。
2.练习能最真实地再现出学生的学习水平。练习中,学生自然会摆出自己经过课堂交流后所形成的个性化的新知识建构内容,这其中会真实的再现出学生的真正“学会”程度,成功、成熟与不合理、错误的情况一览无余。积极地把握练习中的生成资源,课堂会展现出许多新的思路。通过组织学生再次交流与关注,会再次强化水平滞后学生的能力培养,提供提升机会。
3.练习是一些常用思考方式方法的必要训练平台。新课更多地关注解决策略,思维拓展,但就“方法论”而言,“策略层”是核心,“表现层”是外衣,“表现”即借用一定的文字、图形、符号及一些合适的组合形式来表达自己的思考过程。这种表现能力也应该是方法的重要内涵。如一些专用方式:图表法、符号法、集合法,演绎记录程式等。这些技能性的东西要在练习中有机强化训练。本案例中,第一次练习时许多学生的思考是散乱的。为此,教师特意安排了第二次有任务性的再练习。结果孩子想到了列表、归类、整理、符号记录等。在这些良好的表现形式助推下,5种结论大部分学生想到了。
4.练习是“类问题”学习过程的必经之路,也是“类方法应用”“类思维”体验的必由之场。这个环节是真正巩固落实双基、形成能力的空间。本案例中,“长方体长、宽、高”的特点,学生在新课学习时只是经历了特性发现过程,此问题是特性的应用过程。但练习应用知识过程,其实与新课探索中的学习过程是完全不同的,关键在于此过程是以“应用”性思维为主,是新课探索中“棱分组”思维过程的逆向展开。为此,这个过程有其独特具的价值。
(四)应对措施
鉴于此,数学练习应该是“过程与方法”目标达成的有效平台。在实践中尝试“练习过程与习题设计”双关注,以挖掘练习习题及练习过程中的“过程与方法功能”,促进学生真正用起常规思维方法,实现数学思考能力的提高。
1.关注“习题”的类方法训练价值。学生在新课中初试的解决策略,往往建立在对别人思维结果的回思过程中,有很深的他主影响,支架痕迹十分明显。为此,教师往往要设计大量“基础题”,顺学生思路,强化学生新体验;同时,跟进练“变式题”,旨在丰富“类思维”的广度,让学生在多种思想交融中增强自己的理解,发展数学思维。
2.关注“练习”的体验(过程)价值。 练习不应该只是传统意识中一种“习题——生”的简单单向对话,而应该是“问题——学生——教师——同伴”间的多向对话过程。也就是练习要以习题设计为起点,学生、教师、同伴共同介入展开多层面的互动,实现一个多流向的对话过程。前不久听特级教师丁杭缨老师《三角形三边关系》一课,丁老师的练习展开设计与教学行为,让笔者更深体会到练习是教学中落实过程与方法目标的积极有效的过程。丁老师在练习环节只抓住了书本中一道题:
下列每组中的三条线段能围成三角形吗?
(1)______3cm (2)____________6cm
________4cm ____________6cm
__________5cm ____________6cm
(3)_______3cm (4)___________6cm
_______3cm ___________1cm
_______3cm ___________9cm
师:先请大家自己判断(生—— 习题对话)
师:第一组3cm、4cm、5cm三条线段能围成三角形,这三个数据有什么特点?
生:连续的自然数。
师:那说明什么?
生:连续的三个自然数就能围成三角形。
师:是吗?
生:不对,1、2、3这种情况就不对。
师:其他情况行吗?(学生的思维被引爆,对连续自然数这种组成关系的三条线段,学生在老师的引导下进行了深度思考,经历了完整与深刻的体验过程。)
……
师:3cm、3cm、5cm能围成什么样的三角形?
生:有两条边长度是一样的三角形。
师:那这个三角形中5cm线段能换其他长度吗?是怎样长的线段?
生:小于5cm都行。
师:那请你在脑中将这几个三角形画一画,感觉一下分别是怎样的三角形?
生:越来越尖的三角形。
生:越来越窄的三角形
师:你脑中的图形是不量这样的(师电脑展示:)
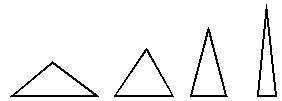
师:能换3cm这条边吗?请试着换一换。
……
纵观丁老师练习组织,可以看出这里不再仅仅是解决一道习题的行动,而是一个新的师、生、习题多向互动的过程。学生不再只是知道两边和与第三边关系,而感觉与体验到了间空图形渐变、区间的发掘。“让每道题尽展多种价值”练习不仅仅是学生解题、老师对答的简单行为过程,而是学生体会与掌握多种学习方法的重要过程。