首页 -> 2007年第9期
高职高等数学教学案例:Lagrange中值定理的教学
作者:熊庆如
关键词:最近发展区理论;教学模式;教学效果
就教学与发展问题,维果斯基提出了著名的“最近发展区理论”。维果斯基认为,学生的发展可以区分为两种水平,第一种水平是现有的发展水平,由已经完成的发展顺序的结果而形成,表现为学生凭借自己的能力独立地解决智力任务。第二种水平表现为学生还不能独立地解决某些问题,但是在外界的帮助下可以解决这些问题。学生独立解决问题时的实际水平(第一发展水平)与教师指导下解决问题时的潜在水平(第二发展水平)之间的距离,就是“最近发展区”。
学生的第一发展水平与第二发展水平之间的状态是由教学决定的,即教学可以创造最近发展区。因此,好的教学绝不应消极地适应学生智力发展的现有水平,而应该走在发展的前面,把学生的智力从一个水平引导到另一个更高水平。
最近发展区理论实际上对什么内容应该由学生先学、什么内容应该由教师后教做出了明确的划分。显然,如果学生要学习的内容在他们的已有发展区(或现在发展区)之内,就应该让学生通过自学来解决;如果要学习的内容落在最近发展区之内,就需要教师的指导或讲授。这样才能最大限度地培养学生的自主学习能力。传统教学一般遵循先教后学的顺序,学生在听取教师讲解的基础上再学习和练习。这种教学的一个明显缺点是对学生的已有发展区和最近发展区不作区分或区分得不好。我们认为,造成这种结果的一个重要原因是教师没有掌握划分“两区”的具体技术。
维果斯基对现在发展水平和最近发展区的解释是抽象的,并没有对如何确定两个发展区作明确回答。要彻底解决这个问题,在“已有发展区”和“最近发展区”的理论上必须有所突破。我们要从具体意义上来理解学生“已有发展区”和“最近发展区”。为了确定学生的两个“发展区”,教师可使用任务分析技术和自学检查法。任务分析是指在开始教学之前,对教学目标中所规定的、需要学习得到的知识或技能构成成分及其层次关系详加分析,为学习顺序的安排和教学条件的创设提供心理学依据。任务分析的基础是知识分类及其层次理论,其内容是确定学生的起点能力、分析学习的先决条件以及支持性条件等。学生的认知发展水平是一个由低级到高级、由简单到复杂的渐进过程,因而我们的教学也必须符合这一发展过程。自学检查是指让学生在教师正式授课之前自学,检查学生自学的情况,然后再确定教学的起点。相比之下,任务分析法对学生“两个发展区”的区分可能更准确一些,也更有利于发挥学生自学的潜能。
结合高等数学的拉格郎日(Lagrange)中值定理教学,在关于“最近发展区”的理论问题上,探索如何发挥学生自主学习的积极性,笔者有如下一些体会:
在讲完罗尔(Rolle)中值定理之后,接着就讲拉格郎日(Lagrange)中值定理。拉格郎日(Lagrange)中值定理的证明就使用了罗尔(Rolle)中值定理。教材关于拉格郎日(Lagrange)中值定理的叙述和证明是这样的:
拉格郎日(Lagrange)中值定律:若函数f(x)满足条件
1.在闭区间[a,b]上连续;
2.在开区间(a,b)上可导;
则在区间(a,b)内至少存在一点x0,使得f′(x0)-[f(b)-f(a)]/(b-a)=0或f(b)-f(a)=f′(x0)(b-a)
证明:如图1所示。
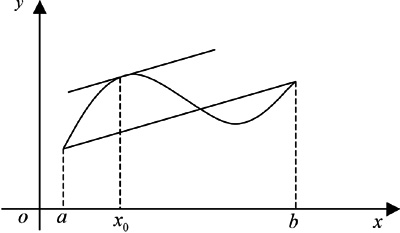
图1
设辅助函数F(x)=f(x)-[f(b)-f(a)]/(b-a)·x,x∈[a,b]
显然F(x)在x∈[a,b]上满足罗尔定理的条件:F(a)=F(b)
于是存在x∈[a,b],使F′(x)=f′(x)-f(x)-[f(b)-f(a)]/(b-a)=0
有f′(x)=f(x)-[f(b)-f(a)]/(b-a)证毕
如果教师按这样的顺序进行教学处理,学生必然会有许多疑问:为什么要构造这样一个函数F(x)=f(x)-f(x)-[f(b)-f(a)]/(b-a)·x,x∈[a,b]?怎样想到构造这样的一个函数?………
对于高职学生来说,构造这样一个函数就犹如一道知识的鸿沟。如何才能帮助学生跨越这一鸿沟?教师的作用就凸显在这里了。
笔者认为,在讲授拉格郎日(Lagrange)中值定理的证明之前可先讲以下几个例子做些铺垫:
例1.已知抛物线y=x2+ax+2,(a∈R)与坐标轴X轴有两个不同的交点。求a的取值范围。(如图2所示)
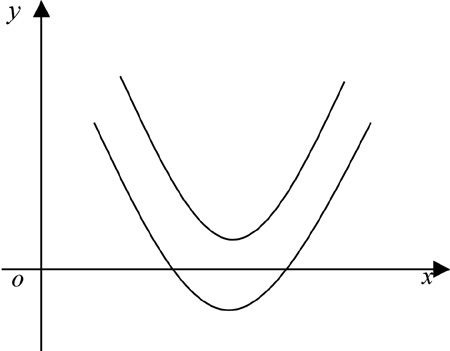
图2
例2.已知点A(1,0),B(3,0),若抛物线y=x2+ax+2,(a∈R)与线段AB有两个不同的交点,求a的取值范围。(如图3所示)
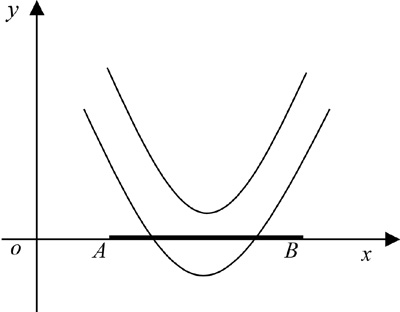
图3
例3.已知点A(1,1),B(3,1),若抛物线y=x2+ax+2,(a∈R)与线段AB有两个不同的交点,求a的取值范围。(如图4所示)
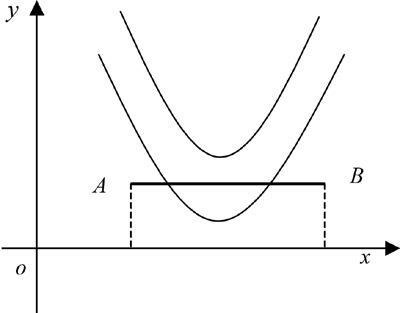
图4
例4.已知点A(1,1)、B(3,3),若抛物线y=x2+ax+2,(a∈R),与线段AB有两个不同的交点,求a的取值范围。(如图5所示)
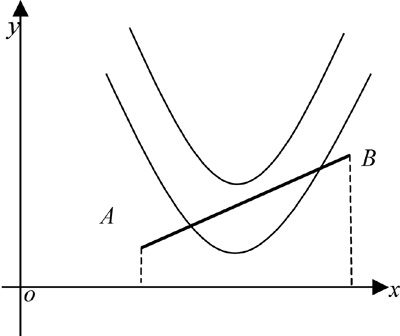
图5
看了此例题之后,学生或许会注意到相邻两个例题的函数区别那么小,但其结果却是相差甚远,原因就是例1是求解例2的基础。同理,例2又是求解例3的基础,例3是求解例4的基础。如果没有例2这个环节,直接让学生完成例3和例4,则学生会有“一步登天”的感觉。按照例1——例2——例3——例4的顺序教学,完全符合学生的认知规律。因为例2的“问题解决能力”是例1的“潜在发展水平”,而例3、例4则是例2、例3的“潜在发展水平”。其间的“最近发展区”在他人的帮助下是完全可以顺利过渡的。笔者在教学实践中体会到,在讲拉格郎日(Lagrange)中值定理的证明前,若把这四个例子作为铺垫,那么拉格郎日(Lagrange)中值定理的证明也就在学生的“潜在发展区”之内了,教学效率也会有所提高。同时,“最近发展区”理论下的数学学习是学生思维从潜在水平开始的,在这里,学生已有知识能力不足以解决所面临的问题,从而激起学生认知上的不平衡,看到自己已有知识的局限,激发他们固有的好奇心,于是能主动地带着问题去学习、研究和探索,去寻求解决问题的办法,并力求在教师帮助下,在集体活动中,通过自己努力,使问题得以解决,达到新的、更高水平上的平衡。
拉格郎日中值定理是微分中值定理中的一个重要内容。它既是罗尔定理的推广,又是柯西定理的基础。就知识体系来说,拉格郎日中值定理在此起着桥梁和纽带的作用。就应用范围来说,拉格郎日中值定理在研究函数应用中有较大的空间。所以,学生学好拉格郎日中值定理,既有利于加深对罗尔定理的理解,又为学习柯西定理打下基础,还有利于后续学习。
总之,通过这样的一个教学铺垫,既加深了知识理解,又活跃了学生思维,同时还培养了学生的探索精神,学生在拉格郎日中值定理方面的解题能力得到了进一步提高。
参考文献:
[1]顾静相.经济数学基础[M].北京:高等教育出版社,2004.
[2]皮连生.学与教的心理学[M].上海:华东师范大学出版社,1997.
[3]李士锜.数学教育心理[M].上海:华东师范大学出版社,2001.
[4]张奠宙,唐瑞芬,刘鸿坤.数学教育学[M].南昌:江西教育出版社,1991.
[5]徐斌艳.数学教育展望[M].上海:华东师范大学出版社,2001.
作者简介:
熊庆如(1964—),江西宜丰人,硕士,浙江省东方职业技术学院讲师。