首页 -> 2007年第1期
例谈数学试题的优化
作者:姚新付
一、 改题型
例1原题我们已经知道:2个10相乘可以记作102,3个10相乘可以记作103。按照这样的方法,105的结果应该是( )。(填空题)
修改:改为选择题,选项为:①1000②10000③100000
说明:原题设计新颖,以学生熟悉的数学知识为条件,问题对学生来说却是陌生的,需要学生依据旧知识总结出“规律”再解决新问题,但作为填空题难度较大。考虑到试题涉及到的数学知识的抽象性和试题本身的新颖性,不妨把其改为选择题,让学生运用估算、排除法等更多策略解决此题,力争达到试题的新颖性和难度性的科学平衡。
二、 改顺序
例2原题用3/8、1/8、3/5、和()可以组成一个比例。括号里的数是()。
修改:用3/8、3/5、1/8、和()可以组成一个比例。括号里的数是()。
例3原题修路队要修建一条4.8千米的公路,计划要用15天修完。实际每天比计划多修0.08千米,实际多少天就完成了任务?
修改:修路队要修建一条4.8千米的公路,实际每天比计划多修0.08千米。如果已知计划要用15天修完,那么实际多少天就完成了任务?
说明:现实生活中的信息和数学问题常以一种散乱的形式进入我们的视野。例2原题一般可以根据比例的意义和基本性质来解答。但更多学生顺着题目“读”过去,易发现3/8和1/8是3倍的关系,很快能得到答案为1/5或9/5,显然,这并非原题设计意图之所在。将数据打乱后,则需要学生利用慧眼通读全题,分析后才能发现3/8和1/8是倍数关系,这也有助于学生利用更多的方法解决此题。例3一改传统的条件呈现顺序,打破学生“经验型思考法”,需要学生对信息进行重新整理,从而促成问题的解决。无论是改变数据顺序,还是改变条件顺序,有时我们还可以改变问题的呈现顺序,都能提高学生解决问题的思维含量,真正考核对知识的掌握和运用技能。
三、 改数据
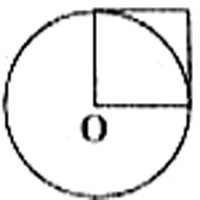
例4原题如右图,如果正方形的面积是16平方厘米,那么圆的面积是()平方厘米。
修改:把原题中的“16”改为“15”。
例5原题打印一份稿件,甲单独打印需要20分钟完成,乙单独打印需要30分钟完成。两人合作需要多少分钟完成?
修改:打印一份稿件,甲单独打印需要1/4小时完成,乙单独打印需要1/2小时完成。两人合作需要多少小时完成?
例6原题规定:a△b=a×(b+2),则5△2=5×(2+2)=20。同理可得,3△8等于()。①24②30③12④50
修改:把5△2=5×(2+2)=20改为5△4=5×(4+2)=30。
说明:有人说,数学题好编,只要变化一下数据,新题目就诞生了。说得不无道理,但却只是表面。例4数据变化后,学生会产生“不好算”的感觉,促使他们寻找其他的解题策略,渐渐发现:原来,求圆的面积不一定需要直接知道圆的半径。这样有效矫正学生对圆的面积公式的机械理解,考察学生思维的灵活性和独创性。例5原为一道典型题——工程问题应用题。在经过一定量的练习之后,学生形成了较为稳固的解题模式,解法即为1÷(1/a+1/b),其实部分学生并未理解其本质:工作效率是工作时间的倒数。他们只是记住了解法的结构。修改后的题则能更为有效地检验学生对工程问题的理解,引领学生不要套用公式,而要仔细分析,灵活解题。例6原题这种“新运算”的题在以前是作竞赛之用的,作为一道水平测试题,虽然新颖,但难度太大。等式“5△2=5×(2+2)=20”里括号中的两个“2”意义并不相同,不妨把其改为“5△4=5×(4+2)=30”,排除不必要的干扰因素,让学生更快地理解新运算的规则,继而解决问题。
四、 改情境
例7原题甲、乙两队合修一段公路,甲队单独修15天完成,乙队单独修10天完成。两队合修多少天完成?
修改1:整理一批图书,张明一个人整理要6小时,李华一个人整理要8小时。如果两人一起整理,需要多少时间?
修改2:一批布,全部做上装可做15件,全部做裤子可做10条。如果成套加工,可以做多少套?
说明:传统的工程问题应用题的情境一般是“修路、做零件、水池进出水、打印稿件”等,学生练习的也大都是此类题。生活中的“工程问题”其实有很多,例如加工服装、整理图书、喝水等。学生对题目的熟悉程度会直接影响他们的思考空间,联系多彩生活,我们可以设计情境更为丰富的试题。例7的情境修改后,加上对“单独、合”等关键字词的修改,问题的思考含量明显提高,对学生来说是一次全新的挑战。
五、 改人文
例8原题6和15的最小公倍数是(),把它分解质因数是()。
修改:6和15的最小公倍数是();把20分解质因数是()。
说明:近年来,命题体现人文性是个热点。例如将试卷版面设计得“趣味盎然”,或将传统的“填空题、判断题、选择题”名称改为“认真审题,准确填空;反复比较,慎重选择;仔细推敲,认真辨析”等亲切型导语,又或是在试卷中加入一些激励性的提示语。笔者认为,这样的关怀有利于学生调整好良好的考试心态,增强学生考好的信心,但似乎还不够,只是停留在表面。例8原题两小题前后关联,答案一错惧错。修改后,试题的独立性更强,从源头处为学生考虑,这是另一种形式的人文关怀。
六、 改形式
例9原题姐弟两人共有邮票140张,已知弟弟的邮票张数是姐姐的2/3。求两人各有邮票多少张?
修改:下面是姐弟两人的对话:
姐姐:“我和你一共有140张邮票。”
弟弟:“我的邮票张数是你的2/3。”
请你算一算,姐姐、弟弟各有邮票多少张?
例10原题五岳名山的海拔分别如下:东岳泰山1545米,西岳华山2160米,南岳衡山1290米,北岳恒山2017米,中岳嵩山1440米。五岳名山的平均海拔是多少米?
修改:五岳名山的海拔如下表:
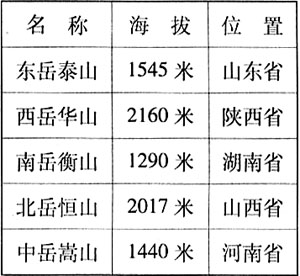
五岳名山的平均海拔是多少米?
例11原题蜗牛5分钟爬行了41厘米。照这一速度,它爬行61.5厘米要多少分钟?
修改:
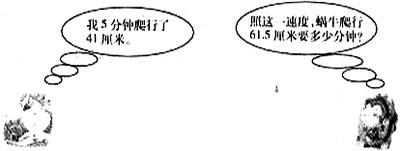
说明:现实生活中许多问题的呈现形式本身就很多样,应用题的表述方式不应只是“纯文字化”的,还可以用表格、图画、对话、情境、资料等形式,把对数学知识或数学技能的检测建立在有趣、生动、新颖的形式之上。立足原题设计意图,三个例题修改后,呈现形式多样化,加上卡通人物,学生读来亲切舒畅,不致使他们陷入对问题的僵化理解,更能激发他们的思考,使学生感到解题也是有趣的。
[2]