首页 -> 2008年第8期
数学教学中教师“反问”的技巧
作者:陈 娟
数学教学中的反问,是老师对于学生的问题,不直接回答,而是将学生的问题加以转化,变成让学生自主探究的问题,是老师应对学生提问的一种处理方式。教师的反问应在学生的提问之后,如他们对知识、方法产生疑问等,教师在面对学生提出的问题时,应机智应对,有的可以直接告诉他们解决问题的方法,更多的是通过教师反过来再问学生的形式,引导学生探究知识。这样可以促进学生对自己产生的问题作进一步深层次的思考,从而达到自行解决问题的目的。
一、 顺水推舟式
通过教师的反问,使问题更加清晰,更具条理,降低了问题的难度,这种反问对知识本身不做任何解释,只是提示学生对知识的认知要全面到位。
案例:“圆的周长与面积”一课。
生1:怎样求出大树离地面1米高的树干的横截面面积?
生2:要求面积就要知道半径,直接量半径。
生3(愤愤不平状):要量树干的半径,不就要把树给砍倒吗?破坏环境!
生4:应用一根绳子先量出树干的周长,再用周长算出半径,然后利用算出的半径求出树干的横截面面积。
师(赞同状):生3、生4你们说的太好了!
师反问:那我们真的就不能直接量出树干的直径或半径,来计算它的横截面的面积吗?
生5问(疑惑状):可以在不破坏大树的情况下测得它的直径吗?
师反问:难道不可以吗?
全体学生诧异状。
生5(惊喜状):我们可以用两块木板夹住大树的树干,再用尺子量出两块木板之间的距离,这个距离就是树干横截面的直径。
通过教师的反问,让学生顺应自己的问题接着思考,从而让学生体验到解决问题的传统方法,通过创新,得到了不同一般的方法。
二、 欲擒故纵式
学生提出的问题具有一定的难度,通过教师的反问,让学生先解决与问题相关的但相对来说较容易的问题,再来研究所要解决的问题,也叫做触类旁通式。
案例:“倍数与因数”一课。
师:自然数可以分为两类:单数(奇数)、双数(偶数)。
生疑问:也可以分为素数与合数吧?
师反问:什么叫素数?什么叫合数?
生答:只有1和它本身两个因数的数叫素数;除了1和它本身还有别的因数,这样的数叫合数。
师反问:1是素数还是合数?
生答:1既不是素数,也不是合数。
师问:自然数还可以怎么分?
生答:1、素数、合数。
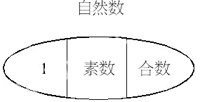
通过教师的反问,让问题越来越小,先是理解概念,然后再为自然数进行分类。这样的反问有利于理清学生对概念认识不透的现状,帮助学生有效地理解概念、正确地应用概念。
三、 方法指导式
学生对知识不能进行有效的应用,不是因为没有理解知识,而是因为没有找到合理的学习方法,这时教师应对学生的学习方法或解决问题的途径给予指点,运用这种方法即可解决提出的问题。所谓:授人以鱼,不如授人以渔。
案例:“公因数与公倍数”一课。
暑假,小红与小明参加游泳训练,小红每三天去一次,小明每五天去一次,他们在7月31号同时去第一次,那么他们第二次同时去是在几月几日呢?
生1:找日历卡,圈一圈就知道了。
生2(无奈状):这样做太麻烦,没有好的解决办法吗?
师反问:你能找到更为简洁的办法吗?
生2:小红去的日期是3的倍数,小明去的日期是5的倍数。
生3(惊喜状):就是求3和5的公倍数。
师反问:有哪些?
生2:15,30……
师问:他们第二次同时去是几月几日?
学生已经认识到用“圈一圈”的方法来解决问题较繁杂,可一时又想不出更好的办法,通过教师的反问,让学生很快就找到了解决问题的捷径,让学生体验到学习成功的愉悦。
四、 点石成金式
学生要解决某一提出的问题,通过教师的反问引导学生先解决这一问题中的问题,再来解决提出的问题;或应用反问的连续性,通过二次反问,使问题变得越来越小,从而达到解决大问题的目的。
案例:“素数和合数”一课。
生问:3是素数,3的倍数一定是合数吧?
师反问:一定是合数吗?
生回答:一定是合数,因为任何两个自然数的乘积就是合数。
师反问:要确定3的倍数是否是合数,先说说3的倍数有哪些?
生1(容易状):3的1倍数是3;3的2倍数是6;3的3倍数是9……
生2(惊喜状):3的1倍数是3,而3不是合数。
师接着反问:任何两个自然数的乘积都是合数这句话对吗?
通过教师的反问,学生对于“任何两个自然数的乘积是否是合数”这一知识点的理解更透彻,不仅达到了解决问题的目的,也显现了知识的衔接性。
五、 追根求源式
教师的反问让学生对所学知识的本质有深刻的了解,促使他们在动手动脑的基础上正确地理解知识。
案例:“环形的面积”一课。
王师傅加工一个环形铁片,它的外圆半径是3厘米,内圆半径是2厘米,请你求出这个铁环的面积?
生: 32×3.14-22×3.14
=(32-22)×3.14
=5×3.14
=15.7(cm2)
师:你能说说怎样求环形的面积吗?
生1:外圆面积—内圆面积=环形面积
生2:(外圆半径的平方—内圆半径的平方)×3.14=环形面积
师:你们总结的很好!
生3(惊喜状)问:环形面积=(外圆半径+内圆半径)×3.14,对吗?因为32-22=5,而3+2=5。
师(出乎预设,但很快平静):他说的好像也有道理,这样的话,我们计算环形面积的公式就变得简单了。
师反问:你能举个反例说明吗?
生举例说明。(共56名学生,列举了形式多样的环形)
师总结出求环形面积的计算公式。
通过教师的反问,生成了求56个不同环形面积的情况,让学生对环形面积的求法不再产生片面性,从而达到让学生准确而又深刻地理解环形面积的计算方法。
总之,数学课上巧用、妙用反问这一修辞手法,也可谓是教师的一门教学艺术。它能使枯燥无味的数学知识更形象、生动、具体;能使单调的课堂气氛充满生机和情趣;能充分调动学生学习的积极性,使学生在欢乐和笑声中获得知识。
责任编辑:陈国庆