首页 -> 2008年第8期
优化呈现方式 满足探究需求
作者:汤卫红
如下图,明华小学到少年宫的图上距离是5 厘米,实际距离是多少米?
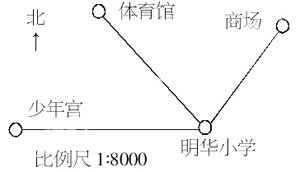
很多教师往往是直接呈现例题,然后审题,并让学生尝试自主解答、交流讨论方法。但一位教师在教学时改变了呈现方式,收到很好的教学效果。
师(首先单独呈现了例题中右边的图):从图中,你能获得哪些信息?
生1:这幅图的比例尺是1∶8000。
师:是谁和谁的比?
生1:图上距离和实际距离的比。
生2:1∶8000表示图上距离是实际距离的
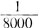 。
。
生3:还可以表示实际距离是图上距离的8000倍。
生4:是把实际距离缩小8000倍画到图上的。
生5:图上1厘米表示实际距离80米。
师:根据生5的理解,我们还可以画出什么比例尺?
生:线段比例尺。
师出示未填写数据的线段比例尺,让学生口头填写。(图上距离1厘米表示实际距离80米,2厘米表示……,3厘米……)
师:除了比例尺,你还能知道什么信息?
生:明华小学距少年宫最远,距商场的最近。
师:你是怎么知道的?
生:在同一幅平面图上,比例尺是一定的。图上距离越长,实际距离也就越长。
师:你真会动脑筋,从图中还能得到什么信息?
生:我们可以量出明华小学到少年宫、体育馆和商场的图上距离。
师:你觉得量的时候,要注意什么?
生6:刻度线要对准表示某个地点的圆圈的中心,这样才能量得比较准确。
生7:也就是从圆心到圆心。
师:我们要找准表示地点的某个圆圈的中心,量出点到点的距离。
学生打开课本测量,然后汇报,教师在图上标出相应的图上距离。
师:现在,你想提出什么问题?
生8:明华小学到少年宫的实际距离是多少米?
生9:明华小学到体育馆的实际距离是多少米?
生10:明华小学到商场的实际距离是多少米?
师:下面请各小组分工合作,想办法算出这三段实际距离,然后交流各自不同的算法。……
思考:
1.变“和盘托出”的单纯接受信息为“崭露头角”的开放式自主收集信息,调动学生主动参与知识建构过程的热情
教材由于编排体例和版面的限制往往采取浓缩呈现的方式,但这并非要求教师“以本为本”,成为忠实于教材的奴隶。事实上,我们不难看出,教材往往给教师留出了较大的“用教材教”的空间,让教师尽可能成为课程资源的开发者。教材并不等于课程。现代课程理论认为:教师、学生、教材的互动和对话才能成为课程。因此,如何呈现教学目标设定的知识,促进课堂的动态生成和学生的主动建构显得尤为重要。上述案例中,例题中所包含的信息是极其丰富的,根据学生已有的知识基础和数学经验是完全能够收集和挖掘的。如果教师忽略这一点,也就丧失了例题教学的很多价值。单纯直接呈现例题,被动地为解答例题去接受题中文字叙述部分呈现的不多的信息,会使学生不去关注平面图中丰富的信息,失去主动探究的热情。可贵的是,案例中的这位教师以前一课“认识比例尺”中学生建构起来的对比例尺含义的多角度、丰富的理解为认知起点,从只呈现包含比例尺的平面图入手,激活旧知,以比例尺为切入点,层层推进,激励学生不断开放式地收集平面图中的信息,甚至挖掘出隐含的信息(如线段比例尺、实际距离的远近)。这样学生所获取的信息量大大增加。既发展了学生收集、处理信息的能力,又为后面求实际距离这一问题出现多样化解法奠定了良好的基础,亦或说学生已经在教师不留痕迹的引导下不知不觉地成为“求实际距离的方法”这一数学知识的主动建构者。
2.变被动解答单一例题为主动提出并解决多个问题,满足了学生自主选择和探究的需求
例题的呈现如果长期采用单一的、封闭式的呈现方式,不但容易使学生失去兴趣,更会让学生形成只会解决现成问题甚至不求甚解、盲目拼凑题中给定条件的不良习惯。因此,充分利用学生自己主动收集的信息,激发学生自主提出问题,并根据具体问题选择需要的信息解决问题,是进行问题解决教学的重要途径,也是克服传统应用题教学中被动接受、机械模仿弊端的必由之路。上述案例中,当学生收集到了比例尺的有关信息、量出了图上距离后,教师引导学生提出有关求实际距离的问题显得水到渠成。收集信息的过程是开放的,获取的信息是丰富的,学生提出的问题亦具有开放性。学生提出问题的过程也是选择、分析、处理已有信息的过程,必然要从众多的信息中寻找有联系的信息,并利用对比例尺的理解提出有关问题。这便从一定程度上发展了学生的问题意识。由于是学生自己提出的问题,同时对问题本身已有相当的认识,所以学生十分愿意选择问题并展开多样化的解决问题的探究过程,呈现在课堂上的将是“百花齐放、百家争鸣”式的解决问题的思路和方法。这些思路和方法源于学生内在的、追寻知识本质的自我实现的需求,是作为“再创造”的成果纳入学生认知结构的,是永不磨灭的。
责任编辑:陈国庆