首页 -> 2006年第2期
高考数学应用题失分原因及对策
作者:李瑛华
一、学生对应用题的认识存在较大偏差,对解应用题存在严重心理惧怕现象
通过与学生的交流,提出如下问题:
(1)说说对应用问题的理解,你喜欢解应用题吗?
(2)解应用题对你最感棘手的是什么?
(3)你了解了哪些解决应用题的方法?
(4)教材涉及应用问题的内容是否过多?过少?
结果分析:学生对应用问题认知结果随认识发展水平的不同也不尽相同;对解应用题的惧怕程度也随着年级的提升逐渐减少。
由于数学应用的广泛性,实际问题背景的多样性,数学应用题往往文字叙述长,数据多而不规则。有的学生读不懂题目,有的学生看不下去,只好放弃,有的学生读了后段忘了前段,怕繁、怕难,学生脆弱的心理、薄弱的意志能力是导致解应用题困难的关键因素。
二、数学阅读能力对解题有较大影响
1.阅读的分析组合能力对解题影响的案例
某电镀厂已受到环保监测部门的警告,如果再不治理环境污染,将从明年1月份起进行罚款,第一个月罚款3千元,以后逐月加罚2千元,在这种情况下,明年生产总收入y(元,按月累计)是生产时间n(以月为单位)的一次函数,且生产一个月收入为7万元。如果现在投资93万元治理污染,治污系统可以在明年1月1日启用,在这种情况下,明年不会受到环保部门的罚款,而且生产收入逐月增长,生产总收入p(元,按月累计)是生产时间n(月)的二次函数,生产一个月收入为10.1万元,生产两个月收入为20.4万元,试问:治污系统启用多少个月投资开始见效?(即治污后的生产总收入p与治污投资额的差不小于不治污情况下的生产总收入y与罚款累计金额的差)
分解题意,把原题改编成:
①若该厂不治污,则明年生产的总收入y(元,按月累计)与生产时间n(以月为单位)的关系式是什么?
②从明年1月起,n个月的罚款累计是多少?
③若该厂治污系统启用后,生产总收入p(元,按月累计)与生产时间n(以月为单位)的关系式又怎样?
④治污系统启用多少个月,投资开始见成效?
结果分析:原题得分率极低,即使是理科班学生得分率也只有0.18,而把题分解组合、改编后,中等以上的学生都能从第一题做到第四题。显然改编后的题目,每个问题中条件与需求清楚,而且前面问题为后面问题起到一定的铺垫作用,这样阅读难度大为降低。原题与分解后的题目有显著性差异。说明阅读分解与组合能力水平低是造成解应用题困难的重要因素。
2.阅读信息处理对解题影响的案例
A、B两个产地分别生产同一批规格产品12千吨、8千吨,而D、E、F三地分别需要该产品8千吨、6千吨、6千吨,各产销地之间每千吨的运价为:从A到D需4千元,从A到E需5千元,从A到F需6千元,从B到D需5千元,从B到E需2千元,从B到F需4千元。怎样确定调运方案,可使总的运费最少?
将以上内容进行信息处理,加工成如下表格
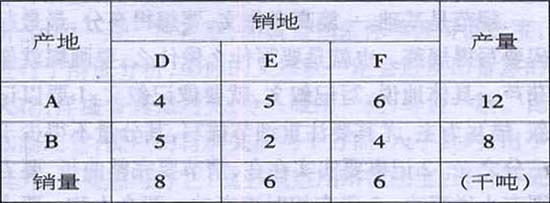
结果分析:原题中条件较多,这就需要学生有较强的信息处理能力。而将上述条件进行整合,将各种条件列成表格后,学生解题得分率明显提高,这表明学生习惯于是线性状态材料的阅读,处理能力水平低下,影响对题意的分析,从而造成解题的困难。
3.阅读策略对解题影响案例
从1999年开始,上海市实施民用多层住宅“平改坡”工程,计划将平顶房屋改为尖顶,并铺上彩色瓦片。现有两种形状的尖顶房:一是有两个面需铺上瓦片,屋脊与房屋等长,如图1所示;二是有四个面需铺上瓦片,屋脊比房屋短,如图2所示。若在相同底面与高的情况下实施“平项坡”工程,哪一种尖顶房铺设的瓦片比较省?
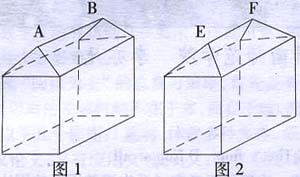
结果分析:图1为直棱柱,图2为过三棱柱一条棱所作的两个截面而成的五面体。由于平行于底面的一条棱的长短与位置均不确定。因此调整策略为可将此棱平行移动,这样本题可归结为如图3中的S△ACE+S△BCES截面ABE的大小问题。对解决本题起到了关键作用。解本题学生遇到困难主要是图2一条棱的长短与位置均不确定,无从下手,说明学生阅读过程中,还需要根据题意调整策略。
三、实际问题转化为数学模型的转释能力偏差是造成解题困难的重要原因
例一:如图4,在一段直的河岸同侧有A,B两个村庄,相距5千米,它们距河岸的距离分别为3千米,6千米,现在要在河边修一抽水站并铺设输水管道,同时向两个村庄供水,如果预计修建抽水站需8.25万元(含设备购置费和人工费),铺设输水管道每米需用24.5元(含人工费和材料费),现由镇政府拨款30万元,问A,B两村还需共同自筹资金多少,才能完成此项工程(准确到100元)。
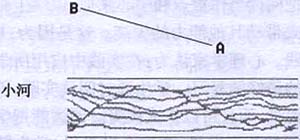
修建供水工程问题,涉及到许多方面,这里仅考虑修建抽水站和铺设户外主管道所需费用。一般同学都认为这是一个代数问题,设CF=x,建立费用y关于x的函数关系为y=根号下9+(4-x)2+根号下36+x2,求y的最小值,但这种无理函数的最值,技巧性强,运算繁杂,如考虑利用立几知识,将问题的关键转化为:在河边上确定点C的位置,使铺设的输水管道AC+BC最短,就不难解决本题了。而能这样考虑的同学显然是少数的。
结果分析:实际问题转化为数学模型来解决,存在着数学模型选择的水平差异,这直接导致应用题困难症结的重要因素。因此注重把实际问题转化为数学模型的转释能力的培养,创新思维习惯的培养是当前提高数学应用能力关键所在。
当然,解数学应用题困难症结并不仅是以上列举的几种,有时出现的情况会复杂得多,有些是我们教师根本无法预料的。这需要我们广大教师在教学过程中不断去了解学生。培养学生的数学应用能力是一项很艰巨的、很重要的工作,需要我们进一步探索研究。为提高解应用题的能力,建议采用以下对策。
1.注意结合学生的实际水平,分层次逐步地推进
数学应用能力培养,对教师、对学生都有一个逐步的学习和适应的过程,教师在设计数学应用题过程中,特别应考虑学生的实际能力水平,起始点要低,应有利于更多的学生参与,提高兴趣。比如在低年级的数学教学中,可以在讲解知识的同时,有意识地介绍知识的应用背景,在应用的重要环境增加较多训练题,逐步扩展到让学生用已有的数学知识解释一些实际结果,到独立地解决教师提供的数学应用问题和一些建模问题,最后发展到能独立地发现、提出一些实际的问题,并能用数学建模的方法去解决。
2.注意结合正常教学的教材内容
数学应用要和现行数学教材有机结合,立足课本,优化教学,把应用和数学课内知识的学习更好地结合起来,而不要乱成两套系统,教师应特别注意把握数学应用、数学建模与学生现实所学数学知识的“切入点”,引导学生在学中用、在用中学。注意培养把实际问题转化为数学模型的转释能力。
3.注意进行抗挫教育,培养学生刻苦、顽强的进取意识
应用题的特点是文字叙述多,数据多,加上学生往往对应用题的实际背景不了解。需要我们教师注重培养学生抗挫能力培养,重点教会学生如何处理各种信息,如何分解原题,如何调整解题策略。特别是开展一些数学交流活动,提高学生阅读能力。切忌数学应用变成老师讲题,学生模仿练习的套路,而应该重过程、重参与,更多地表现活动的特性。
(责任编辑 刘永庆)