首页 -> 2007年第5期
新课程下的主体性与主导性如何把握
作者:郝四柱
1.与学生认知过程相结合。
随着新课改不断深入,课堂逐渐从封闭走向开放,学生从被动走向主动,学生的能量开始释放出来,课堂上产生很多的超越书本和资料的内容,由于认知水平差异,师生互动中难免会出现一些疑问。
课例1:别让“疑问”变“遗憾”
题目:一道开放题:内角为72°和108° 的菱形,请将它分割为四个等腰三角形?
大家经过思考,在黑板上提出许多方案;其中有一些方案如图。

对于图(6)陈笑同学在下面嘀咕:怎么有点不象等腰三角形啊?
我愣了一下,也觉得有一点不象;大家都安静下来。
我叫画此图的王慧同学上来说明一下,她上来标出了各角的度数,说:△ABE、△BEF、△EFD、△FDC的角度数可知它们都是等腰三角形。
我问大家对不对?
大家异口同声地说:对。
我说:我还是觉得不像等腰三角形;
薛飞同学说:要是图形画准确,它就像了。
为了不影响教学进度,我也没多思考,默认了薛飞同学说法,这个问题就这么过去了。
下课了,回到办公室,我想:画个准确图形看看是否正确。通过动手画图,结果证明王彗同学作法是错误的而且能够证明。
根据王彗同学标的角度可知:∵ △ABE≌△BEF、△BEF≌△EFD 、△EFD≌△FDC 、△ABE ≌△FDC
那么AE=BF=ED=FC=1/2AD=1/2AB=1/2CD=1/2FD,这说明下图结论成立
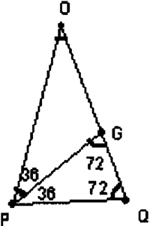
(1)1/2PO=1/2OQ=PQ,
(2)∠O=36°、∠OPQ=∠Q=72°
而事实上PQ≈0.618OP,显然矛盾;因此王彗同学作法是错误;但此时PQ≈0.618OP学生还不能领会。
第二天,为突出错解的纠正,我专门以“天大的谎言”为主题,叙述了王彗同学解法的错因,并换用反证法让学生理解:(如图)
作∠OPQ的平分线PG,∠OPG=∠O =36°∴ PG=OG
∵∠PGQ=∠Q=72°∴ PG=PQ,
∴OG=PG=PQ,∵PQ=1/2OQ=OG,∴OG=PG=PQ=GQ ;
∴△PQG为等边三角形,∴∠Q=60°与∠Q=72°矛盾
大家兴趣盎然地听完我的讲解,恍然大悟,对于“天大的谎言”最终解决抱以欣喜的微笑。
很快,期末复习时我想借此题来强化思维严密性,把感性与理性相结合;然而我让大家回忆“天大的谎言”这一课时,大家忘了题目(包括王慧同学),经过场景提示,只记得有一个菱形和一个错误的方法,至于错在什么地方更无从谈起。
一个很好的具有挑战性的数学探索素材,其最终效果几乎为零。
思考:
(1)讲授法这一课堂教学常用的方法使用时应具有针对性。对于本题这一类具有挑战性的问题,用讲授法学生体会不到“顿悟”那一瞬间的欣喜甚至刻骨铭心的回忆。其效果是:蜻蜓点水,无法深化理解,学生很快遗忘;用这种教学方法要想应试得高分,只能靠反复练习与机械记忆,费时费力不说,这样长期下去,学生那里还有激情与热情去主动学习?
(2)教师教学中要体现出过程性。对于一些同学有价值的疑问、猜想、解决思路等素材,通过教师快速提炼,再返回给同学们,从同学中来,到同学中去,使课堂成为全息世界的缩影。薛飞同学说:“图形不准确,要是图形画得准确就像了”仅仅作了猜想,而没有证明,只需让大家画个准确图形,是非对错一目了然,通过验证、分析、深入思考、问题解决,题目的挑战性就体现出来了。
(3)课例的开放只停留在同一层次水平上,来变换不同的构图方式。知识没有拓展,能力没有得到进一步的提高,为完成课堂预案而教学,没有挖掘并及时纠正课堂中出现的错误,学生失去自主探索、研究的一个绝好的机会。对于一些同学的疑问,要发挥教师的引导作用,让全班同学发现疑点所在,调动积极因素进行思考,使学生对知识的理解融会贯通,让疑问变为强化知识理解的导火索,把疑问变成优秀的课程资源来开发利用。
2.与知识发散方向相结合。
随着课堂开放,教学中会出现很多信息,其中不乏闪耀着光辉的珍珠。通过抓住学生中间稍纵即逝的偶然信息进行有价值的发散,那么课堂上的课程资源会像涌泉一样,用的越多,涌出的就越多。
课例2:实数概念一节
学生寻找规律兴趣盎然,思维通畅,课堂气氛活跃,效果良好。
思考:本人从课例2中发现了价值很高的发散点后,没有回避、更没有扼杀,而是大力表扬学生的发现,激发学生表现欲望,进行创造性学习,通过教师的引导,对知识点进行深入理解,得出勾股数规律,挖掘了教材,使知识融会贯通。在数轴上进行无理点构建之后,说明数轴上无理点它像有理数点一样有无数个,为实数与数轴上点一一对应做了充分准备,顺理成章,毫无牵强附会之感。实数概念这一节,单调抽象,枯燥无味,但对于学生中有价值的发散点有效利用后,大家顺利接受了实数这个抽象概念;我深感:即使有时花的时间多一些也值得,因为抓住课堂闪光点,调动学生积极性之后大家在学有用的数学;促进了学生主动思考、勇于创新的意识,达到知识、态度与能力的共同提高,完全符合新课程理念。
3.与新课程理念相结合。
数学的核心是思维的深化与能力的发展,数学终极目标是可持续发展,如何实践新课改精神,需要教师在课堂教学中把握一个原则:加深理解知识的同时,更要培养能力(包括创新能力)。
课例3:将长为3 ,宽为1的矩形分成相似的三个部分,如何分割?
由于本题涉及矩形相似这个概念;我叙述矩形相似,四边形相似,多边形相似概念,很多学生分别把长与宽三等份并作对边的垂线的二种方法很快解决了问题。
戈奇玉同学说:我看这样行不行:
思考:从题目要求来看,本题已经解答,可以不再深挖;但从能力来讲,这是提高学生能力素质的最佳时机,切不可错过,不能就题解题,仅用应试的观点来看待问题,教师主导性与学生主体性发生冲突时,应让位于学生主体性,从学生能力方面入手,对能力的要求上不封顶。若戈奇玉说对了很好,说错了也不要紧,再纠正,纠错一直伴随知识掌握的全过程。由于他的精彩表现,同学们不由自主的鼓掌叹服。大家从戈奇玉身上学到了许多情况下学不到、学不好的东西。
我顺势问:还有其他的方法吗?
在戈奇玉的带领下,经过同学们认真思考,又发现了几种方法:
4.与学生个性特点相结合。
好的解题方法与好的教学方法应建立在主体的基础上,与学生的个性相结合。
课例4、已知△ABC,三边为a,b,c且a2+b2+c2-ab-bc-ca=0判断△ABC的形状。
[2]
本文为全文原貌 请先安装PDF浏览器
原版全文