首页 -> 2007年第8期
新课程背景下数学考试命题初探
作者:唐文建
(一)试题内容要注重基础知识和基本数学思想方法的考查
《数学课程标准》所规定的学习内容和要求是基础的、具有发展性的,是对学生数学学习的一个基本标准,是多数学生应达到的标准。突出基础性主要表现在以下几个方面:第一,严格按照《数学课程标准》的要求命制试题,不能扩大范围和提高要求:第二,试题应突出对基础知识、基本技能和基本的数学思想方法的考查;第三,在严格控制总题量的情况下。试题应尽可能多地涵盖《数学课程标准》所规定的学习内容;第四,试题应关注《数学课程标准》各目标领域核心内容的考查。例如,函数与方程的思想、分类讨论的思想、数形结合的思想、化归与转化的思想和配方法、待定系数法等在命题中应重点予以关注。
(二)命题构思要注意整体性
一套好试题决不是各个小题的堆砌,它应整体性地反映当次考试的目的和理念,这一点在构思中就应注意把握。有一些程序操作性的数学技能和特殊的数学解题技艺,往往要用强化训练方式获得,其数学应用和智能开发的价值并不大,而避免在考试中涉及、要淡化特殊解题技巧、强调用通法。要从考试源头上削弱过度训练、题海战术的做法;要整体性地把握知识技能和阶段要求以及终结要求,避免“人工催熟”式的超前要求和超前考试,尊重学生发展的阶段性和数学能力的过程性。如,代数计算的难度和空间与图形中推理的要求,在考试试题中的目标难度不能超过教科书复习题的相应难度。
考试的数学期望一般用及格、高分率、均分三项指标反映。随着考试性质的不同这三项期望值有所不同,如:“中考”的高分率期望值与高中招生率高度相关,随着近年来高中招生规模的扩大,高分率期望值逐渐加大。命题构思对这三项期望值应有整体性考虑,平时期中、期末试的及格率80%以上,高分率35%以上、平均分70(百分制)以上;中考的及格率70%以上,高分率20%以上、平均分65(百分制)左右比较适宜。这几项指标定的过低,将会明显加大学习竞争并引发过度的机械性解题训练,特别要防止出现加大考试难度造成期望指标过低而引发对新数学课程的责难。
考试的“区分度”是一柄双刃剑,一方面考试内在的甄别功能决定了任何考试都存在“区分学生”,有些考试(如中考)更是“区分选拔”的要求较强;另一方面过度地“区分”,如,强调“一分之差”的准确无误等,必然会降低数学教学的活力,将教与学从重数学过程引向重数学解题过程。义务教育阶段的各种考试(包括中考),都应起点不高、难度为平台式上升,“区分选拔性”题目的个数适当、分数要少。从一个群体来说,略为降低一点区分度,可以为教与学带来生机与活力,提升整个群体的学习数学的兴趣,给创新性人才提供了发展的空间。
(三)编拟试题要注重开放性
考试的开放性体现在两个方面,一是考试方式;二是考试试题内容。考试方式的改革已有很多做法,如,将长周期作业、研究性学习课题纳入到考试范畴和记分,这些无疑是很有价值的,但还难为一般人(社会)的普遍认同。开放性试题,对考查学生对数学知识的理解深度、考查学生创新意识等方面起到了积极的作用。如:
例1写出一个以-2和4为根的一元二次方程__________________________
例2小英对代数式3a给出了这样的解释:西瓜每千克3元,那么买a千克西瓜,共需要3a元,请你对该代数式作出另外的解释是________________
(四)试题的内容特征要注重实践性和数学生活化
《数学课程标准》特别强调数学背景的现实性和“数学化”。以学生熟悉的现实生活为问题的背景,让学生从具体的问题情境中抽象出数量关系,归纳出变化规律,并能用数学符号表示,最终解决实际问题。
新的数学教材在数学生活化方面给出了范例,使得教与学都对数学的认识更全面,看到了现实世界中的数学,这对绝大多数不会终身从事数学工作的学生来说,无疑是好的,学生测评应与之相适应,使考试试题的特征突出实践性。这里的实践性与那些需要长时间完成的课题学习不同:一是避免涉及实际的问题全部过难或者过易,应高中低档题目都有;二是尽量不超过已学知识的范畴。或是能用已学知识在短时间解答;三是除题目的背景来源于实际生活,使学生感受到“处处有数学”,是学生身边的数学,如,除了选材于实例的“打折销售”外,还有其他范例:
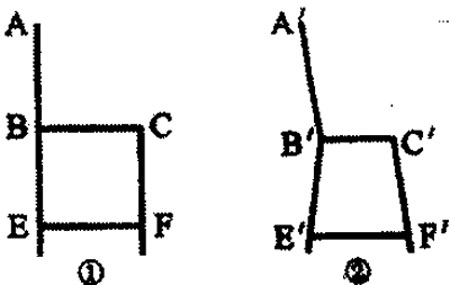
例1用所学数学知识去解释或观察生活中的试题(如图)家俱店中卖的椅子一般设计成图②形状,而不设计成图①形状,因为图②的椅子比图①稳定、舒适、美观,请你用所学过的角、线段、直线及其位置关系等知识,仿照已给出的不同点,比较①、②两种椅子的不同点后填入下表(不考虑两个椅子的大小)。

(五)试题内容要注重教育性
一套试题的内容。包含了对数学和数学教育的价值判断,不同时期的试题对数学的教育性有不同要求。新数学课程下的数学试题应与时俱进体现出时代特征,陈旧与僵化的技能技巧和与实际相背离的一些数学应用问题,都不应当再纳入试题范围。在设置与实际相联系的数学问题中:一要注重真实性,使学生受到怎样“用数学”的教育;二是正视试题的背景,应以正面的教育影响为主,特别是选取学生能感受到的有影响的题材,这样通过考试可以加倍放大其思想教育价值,如:
例1据《中国国土资源报》2005年4月22日报道:目前我国水土流失面积已达367万平方公里。且以平均每年1万公里的速度增加。设我国水土流失总面积为y(万平方公里),年数为x,则y与x之间的函数关系式为____________,如不采取措施,水土流失的面积按此速度增加,那么到2025年度。我国水土流失的总面积将达到_________万平方公里。
例2为了支援沿河、松桃两县实现两基达标,铜仁某单位为这两个县捐款的情况如下表:
该单位平均每人捐款___________元;

该题的特点是:通过真实的情境,在解决问题的过程中渗透教育,其教育价值体现得恰到好处。在体现数学试题的教育价值方面,我们应注意两点:一是要防止生硬的灌输;二是要防止考查的数学内容为情境服务,使知识性、教育性难符其实。
(六)试题内容应注重学生数学活动过程的
[2]