首页 -> 2008年第7期
小学数学教学中有效自主探索的实践与思考
作者:应淑春
[关键词]自主探索 欲望 方法 实践
《义务教育数学课程标准》(修改稿)指出:自主探索是小学数学的重要学习方式之一。现代建构主义也认为:学生知识的形成不是老师简单的传授,而是学生自己建构知识的过程。现在的课堂教学强调学生是学习的主体,但自主探索学习大多数仅仅是学生提出问题,在短短的课堂交流中解决问题,老师只是给了学生民主权,和以学生为主体的自主探索的学习还有差距。学生学习现状不仅没达到自主,而且事实是唯教师是从、唯教材是从、唯参考答案是从、唯考试是从。如何在小学数学学习中有效实施自主探索,笔者结合自己的教学实践与思考,试从以下几个方面加以阐述。
(一)欲望:自主探索的基础
小学生具有好奇、好动、好胜等特点,容易激发和推动他们自我探究的兴趣。要培养学生的探索精神,教师首先要根据儿童的情感心理特点有意识地创设情境,做到“以境激情”,给学生以新异的刺激感受,变单纯、枯燥的数学问题为活生生的问题情境,吸引学生的注意力,激发其学习兴趣,诱发他们的探索欲望。
1.创设情境,激发探索欲望。良好的情境有助于激发学生探索新知识的积极性,诱发他们的探索欲望。如学习“乘法的初步认识”时,运用多媒体出示童话城堡图。
师:这是童话城堡,想进去吗?但你们必须闯过第一关,提出:用几根小棒摆一个图形,摆了这么多图形,一共用了几根小棒?你是怎样列式的?
学生1:6+6+6+6+6;
学生2:4+4+4+4+4+4;
学生3:3+3+3+3+3+3+3+3+3+3+3+3。
师:看到这些算式,你想说什么?
生1:都是加法;
生2:都有好几个加号;
生3:加数都一样(分别请学生说出每个算式的相同加数是几,有几个这样的相同加数相加)……
师:假如有100个3相加,用加法算式表示你感觉怎么样?(太长了,太麻烦了)能不能用一个简单的算式来表示呢?(以引起学生的好奇心,激起学生的探究和创造的欲望。)
在巩固练习环节,再出示这样两道加法题3+2+4= ,5+4+3+5+3= ,然后问:同学们,这两道题你能改成乘法算式吗?
又一次引起学生的探究兴趣,接着让全班学生分小组进行讨论。在讨论过程中,有的学生说不能,有的说可以,讨论气氛十分热烈,每个学生各抒己见,充分发表自己的意见和见解,通过交流汇报,结果学生一致认为能改为乘法算式,理由是用“移多补少”的方法把几个不相同的数变为几个相同的数,如3+2+4=3+3+3=3×3,5+4+3+5+3=4+4+4+4+4=4×5,通过讨论,又一次点燃学生的思维火花,激起学生的探索欲望,同时也培养了学生的创新意识。
2.挑战提问,激发探索欲望。古人云:“学起于思,思源于趣。”教学中设置疑问,不是为了难倒学生,而是要激发其探索知识的兴趣与热情,产生自主探索的内驱力。例如,学习了长方形和正方形的面积之后,为了让学生进一步理解面积与周长的关系,老师可设问:两个长方形周长相等,面积也一定相等吗?两个长方形周长不同,周长长的四边形面积就一定大吗?边长为4米的正方形,它的周长与面积相等吗?学生在展开讨论的过程中,不仅正确解答了问题,而且还主动设计了许多计算周长和面积的题目,进一步巩固了对公式的理解和记忆,发展了学习的主动性,提高了自主探索的有效性。
3.动态生成,激发探索欲望。新课程的课堂教学是一种开放性、多向性的信息交流活动,有师生之间的,也有生生之间的。要使课堂教学始终在学生情绪的最佳状态中进行,课堂教学中的一切活动就应使学生兴趣盎然,有启迪学生思维的效果。通过学生的质疑问难来推进教学,使其认识逐步深化便是其中一种重要手段。例如,教学“可能性大小”时,学生已经理解了转盘上转动一次的中奖可能性是十分之一。有位学生提出了如果转两次,那中奖的可能性是多少呢?有学生认为是十分之二,有学生觉得不对,有学生认为转4次也并不一定能中奖……通过交流争论大家才认识到:第一次转过后的中奖率在第二次转时就没有用了,第二次转的中奖可能性也是十分之一,因此,概率是不能累计计算的。该教学策略的特点是通过及时抓住学生的提问,并顺着学生的思路延伸下去,通过步步追思,从而生成新知教学的深化点,它是“教学要顺着学生的思路来组织”教学观的体现。
(二)方法:自主探索的关键
关于提高学生的探索能力,达尔文有一句名言:“最有价值的知识是关于方法的知识。”数学思想方法是解决数学问题所采用的方法,它是数学概念的建立、数学规律的归纳、数学知识的掌握和数学问题解决的基础。人们在数学研究中,最有用的不仅仅是数学知识,更重要的是数学思想方法。如何才能有效地授之以“渔”,并使其“得法”,渗透自主探索策略呢?
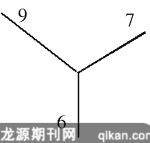
1.运用联想,引发想象。想象是思维的翅膀,没有想象力的学生很难有创造性探索思维。如在教学“长方体认识”时,师出示右下图,问:看到相交于同一顶点的三条棱,你想到了什么?学生想到这个长方体的长、宽、高各是多少?想到了长方体中最大的面是哪两个面?面积是多少?最小的面是哪两个面?面积是多少?想到了这个长方体如果画下去,看到的是哪三个面,看不到的是哪三个面等,学生的思维一下子被激活了。这种训练学生的联想能力,有利于学生自主探索意识的培养。
2.数形结合,化难为易。数和形是数学研究的两个主要对象,两者既有区别又有联系,互相促进。所谓数形结合的思想方法就是通过具体事实的形象思维过渡到抽象思维的方法。数形的结合是双向的,一方面,抽象的数学概念、复杂的数量关系,借助图形使之直观化、形象化、简单化;另一方面,复杂的形体可以用简单的数量关系表示,用图解法分析问题就是运用这种方法。例如教学求比一个数多(少)几的数反叙应用题,例题“南庄小学秋季种树53棵,比春季多(少)种8棵。春季种树多少棵?”先让学生找到关健句,弄清谁与谁比,谁多谁少,画出线段图。这样做学生比较容易找到数量关系,列出正确算式,同时克服见“多”就“加”,见“少”就“减”的思维定势。又如数学广角中的重叠问题,在一次测验中,某班的35名同学中答对第一题的有25名,答对第二题的有23名,两题都答对的有14名,那么有几名同学两题都没答对?解答这道题时,先引导学生借助集合图帮助他们理解题意,搞清数量关系和逻辑关系,化难为易,从而使学生正确列式解答。如下图所示,根据题意,把这35名同学分成4种情况:①表示只答对第一题的同学;②表示只答对第二题的同学;③表示第一题和第二题都答对的14名同学;④表示第一题和第二题都没有答对的同学。

①+③表示答对第一题的25名同学;③+②表示答对第二题的23名同学;根据题意可得①+②+③+④=35,即(①+③)+(③+②)-③+④=35,25+23-14+④=35,解得④=1,即有1名同学两题都没答对。
3.运用“化归”,巧妙转换。化归思想能增长学生智慧与探索能力,是数学中最普遍使用的一种思想方法,即先挖掘内在联系,把问题A转化为熟悉的问题B,再通过问题的解决方法去获得问题A的解。这样做能把问题化难为易、化生为熟、化繁为简、化整为零、化曲为直,可以促使学生提高解决问题的速度。如人教版第八册《植树问题 》:同学们在全长1000米的小路一旁植树,每隔5米栽一棵(两端要栽)。一共需要多少棵树苗?为使学生对“简化”思想和“转化”策略体验得更深刻,把教材原题的“100米”改为1000米。这样做更能突出“繁”,让学生感受到“繁”,才有“化繁”的观念。待学生猜想答案呈现不一致后,通过对直接画图验证的不现实的体验,需要取小单位量来研究,如把1000米看作25米、20米、15米等。让学生领悟到“复杂问题从简单例子入手”,让学生明白碰到复杂问题时可以列举简单的例子来进行验证的转化思想。
[2]