首页 -> 2006年第7期
让抽象变得显然
作者:李尚志
我在20年以前开始讲“线性代数”课时就开始建设这门课程了,“数学实验”是1997年开始建设的,在建设这两门课程的时候都不可能知道教育部以后要评精品课程。那时建设课程的目的就是努力把学生教好。不是为了评选精品课程而是为了教好学生,这就是我建设精晶课程的经验。因此,如果我的讲课能够对于学生产生好的教学效果,就是我感到最欣慰的事情。
有一位学生在网上发了一个帖子,题目是《大学时代影响我的人生的10件大事》。我不知道他是谁,只看得出他以前是学计算机专业的一个学生,听过我的课,现在美国留学,仍然学计算机专业。他所说的“大学时代影响我的人生的10件大事”中,有半件就是“选修了李尚志教授的‘线性代数’课”。他这样描述我讲的这门课程:“复杂抽象的概念和理论经过他的描述,似乎成了显然的东西。”
“线性代数”是大学最重要的基础课之一。比起另一门最重要的基础课“数学分析”或“微积分”来,“线性代数”的内容要少得多。但不少学生感到学起来并不容易。主要困难是太抽象。比如,微积分中的导数可以理解为切线的斜率、运动的速度,定积分可以理解为求图形的面积、由速度求路程,这都比较自然,容易理解。而线性代数从一开始就是一个接一个复杂抽象的定义,好象从天而降狰狞可怕的妖魔鬼怪。比如:行列式为什么要这样定义?矩阵为什么要这样相乘?向量到底是有方向和大小的量,还是数组,还是定义了加法和数乘的任意非空集合中的元素?线性相关、线性无关是什么意思,有什么用处?都是这样的妖魔鬼怪。
作为一个长期讲授线性代数课程的教师,我努力要做到的一件事就是要让学生明白:这些表面上复杂抽象的概念和理论,其实都不是妖魔鬼怪,并不狰狞可怕,而是和蔼可亲平易近人的。这些概念和理论,都是为了解决一定的问题应运而生的,是自然而然产生的。
从这个学生的体会中,我高兴地看到,我的这番努力至少在他身上达到了预期的目的。我是怎样达到这个目的、产生这样的效果的?下面是在我编著的“十五”规划教材《线性代数》(高等教育出版社出版)的前言中选取的一些主要内容,可以说明我的指导思想和具体做法。
一提起抽象,给人的印象就是莫名其妙、晦涩难懂、脱离实际、没有用处,总之是一个令人害怕的贬义词。然而,抽象并不是线性代数特有的,也不是从大学开始的。比如,幼儿园的小孩就要学3+2=5,这是抽象还是具体?怎样教小孩3+2=5?是先教加法的定义,然后再按照定义来做3+2=5吗?加法的定义,幼儿园没教过,小学和中学也没教过,然而小孩们却学会了加法。不是靠定义学会,而是通过例子学会了加法。比如,可以教小孩数自己的手指来学3+2=5,3只手指加2只手指就是5只手指。也可以数铅笔,3支铅笔加2支铅笔就是5支铅笔。假如已经数过了手指,又数过了铅笔,一个细心而胆大的小孩发现手指是肉做的,铅笔是木头做的,举手问老师:“5是肉做的还是木头做的?”老师怎样回答?假如又数了5个乒乓球,发现手指和铅笔是长的,乒乓球是圆的,再问:“5是长的还是圆的?”老师又怎样回答?也许老师会斥责这个不听话的调皮小孩:“好好听课,不要胡说八道!”。然而,这样的小孩才是聪明的小孩,会思考的小孩。他注意到了5只手指、5只铅笔、5个乒乓球的差别,这确实是聪明的表现。但只是注意到差别还不够,还要让他忘掉这种差别,忽略这种差别,将肉做的5只手指、木头做的5只铅笔“混为一谈”,将5个长的物体(手指和铅笔)和5个圆的物体(乒乓球)“混为一谈”,忽略它们的差别而只关心它们的共同点:数量的多少,这才学会了3+2=5,这才能够将3+2=5用到千千万万的其他例子中,如3本书加2本书,3张桌子加2张桌子等。要让小孩学会忽略这些差别,不是一件容易的事情。这正如郑板桥说的:“聪明难,糊涂亦难,由聪明而糊涂尤难。”这种忽略差别的过程,就是“由聪明而糊涂”的过程,也就是数学的抽象的过程。抽象不是从天而降,而是来自于实际,来自于具体的例子。然而,抽象又没有停留于实际,而是“脱离”了实际:它脱离了具体的例子,舍弃了不同例子的不同点而提取了它们的共同点,这样才能应用到更多更广泛的实际例子中。有一个电视节目的时事评论员常说:“许多看似不相干的事情,其实都是相互关联的。”我们可以说:“许多看似不相同的事情,其实都有共同点。”从不同的事情中发现共同点,研究共同点,得到放之四海而皆准的真理,用到更多的不同事物中去,这就是抽象。这样的抽象不是没有用处,反而是神通更广大。数学由低级到高级的过程,就是抽象的程度由低到高的过程,也是应用的范围由狭窄到广泛的过程。幼儿园的3+2=5忽略掉了大小、长短、原料的差别,只关心数量的多少。初中的(a—b)2=a2+b2-2ab将字母a、b所代表的数的多少也忽略掉了,只关心它们的共同的运算规律。更进一步的“糊涂”是:公式(a—b)2=a2+b2-2ab中的字母a、b可以不代表数而代表几何向量,将其中的乘法理解为向量的内积,公式照样成立,画出有向线段来表示公式中向量,如下图:CA=a,CB:b,则BA=a-b则公式(a-b)2=a2+b2-2a·b的几何意义就是|BA|2=|CA|2+|CB|2-2|CA||CB|cosC
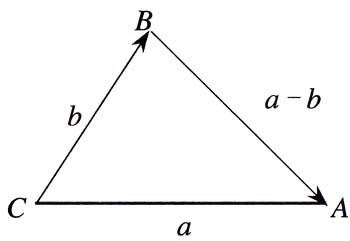
这就是余弦定理!当C是直角时就是勾股定理!只不过一念之差,在乘法公式(a—b)2=a2+b2-2a·b中“难得糊涂”,将数与向量“混为一谈”,就立即得到了余弦定理和勾股定理,数学的抽象的威力由此可见一斑!
我在念研究生的时候,导师曾肯成教授经常给我们指定一些经典著作让我们读,并且轮流到讲台上去讲,他在下面听,向讲的人提出各种问题。通常他并不问某某定义怎样叙述、某某定理怎样证明,而是问:“书上为什么要写这个内容?不写可不可以?”这样的问题很难回答,但我们不得不努力去思考怎样回答。假如我们在讲线性代数时问:“书上为什么要写矩阵和向量空间?为什么要写线性相关和线性无关?可不可以删去?”应当怎样回答?前人在发明这些内容的时候都是为了解决一定的问题。写进教科书中的内容,更是经过历史的检验被证明是最重要最有用的东西。课本上的定义和定理的叙述,每一句话甚至每个字都是经过多少年多少人的反复推敲得到的,字字值
[2]