首页 -> 2007年第1期
高职院校实施数学实验课程的研究
作者:王积建
在实验结束后,凭借期末考试成绩,利用独立样本T检验对实验班和控制班进行统计分析,结果如表1所示。
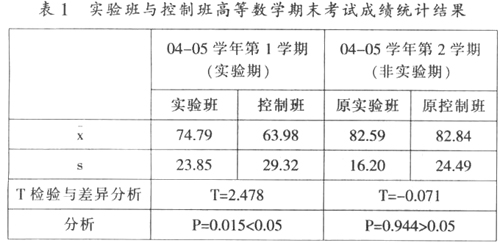
从统计结果来看,在实验1个学期后,实验班的平均成绩明显高于控制班,标准差明显低于控制班,且在0.05的水平上有显著差异。说明数学实验课程对于提高学生的数学能力是有明显效果的。但当实验结束后,经过1个学期的学习,原实验班的平均成绩与原控制班几乎相等,在0.05的水平上无显著差异。对这一现象可做如下解释:在第1学期,实验班和控制班都学习微积分,在第2学期都学习线性代数,而微积分和线性代数的数学内容、思想和方法相去甚远,因而实验班学生在微积分学习中养成的积极情感,在后续的线性代数学习中所发挥的积极影响并不大,所以在第2学期(非实验期)两班成绩无显著差异就不足为奇。
(三)学生参加数学建模比赛获奖情况
从2005年6月开始建模培训到2005年10月参赛,浙江工贸学院首次参加全国大学生数学建模比赛,从研究对象中选拔组建了3个组参加比赛,共获得浙江省2个一等奖,1个三等奖的好成绩。结果表明,数学实验课程对于提高高职学生的数学应用能力和创新能力具有显著的效果。
讨论
(一)关于教学目的
目前,高职院校学生的学习目的主要是掌握职业技术,对数学这样的基础理论课,学习动机不强。许多教师对高等数学教学的理解仍然停留在传统的意义上,即教师是施教者,学生只是被动的受教育对象;教师的教学目的是帮助学生通过考试,而学生学习数学也只对考试成绩感兴趣。结果是,学生难以将所学数学知识用于解决实际问题,课程结束后,没有人再对数学感兴趣。“数学无用”是学生的一种普遍心态,更是学困生弃学的主要原因。
随着科学技术不断发展,各门学科都呈现出“数学化”的趋势,而在传统课堂教学中,教师并没有将这种“数学化”的结果和趋势展示给学生,所以,学生产生“数学无用”的错误认识的重要原因在于教师。数学实验从数学知识出发,利用计算机软件,与其他学科相融合,实现数学知识的再学习和深化。因此,数学实验课程的教学目的就是使学生充分利用计算机技术,提高动手能力、数学应用能力,以及解决实际问题的能力。数学实验是改变应试教育,实现素质教育的有效途径。
(二)关于教学内容
目前,“掐头去尾烧中段”是人们对高等数学教学的普遍概括。而在高职院校,“中段”进一步简化为“计算”,“数学计算”成为高等数学教学的主要内容,甚至是唯一内容。从浙江工贸职业技术学院近三年的数学考试题来看,考试内容几乎全部是计算题,没有考过一道证明题或者应用题。数学是从哪里来的,数学又到哪里去?学生全然不知。难怪学生是只为“应试”而学!有些教师为改善教学而引进了各种CAI软件,即使这样,教师从事的仍然是“数学计算”。高职院校高等数学的改革突破“数学计算”的框框迫在眉睫。90年代以来,许多学校开展的数学建模教学和数学建模竞赛活动是“数学应用”的有益尝试,在此基础上开设的数学实验实现了数学建模与计算机技术的结合,是“数学应用”的进一步提高。但是,高职院校的理论课时在呈现压缩趋势,现阶段不可能增设数学建模课程或数学实验课程,充其量只能以选修课的形式开设,这样只能满足一部分学生的需求,而大多数学生仍然体会不到数学的“来龙去脉”。可行的对策是,对高等数学进行课程改革,将数学内容与实验内容进行整合,删除传统内容中的“繁、难、偏、旧”的内容,增加实验内容,突出数学的来源和应用,教会学生利用数学软件处理繁杂运算的能力、探索数学的能力和解决问题的能力。
(三)关于教学方式
传统教学方式是课堂教学“满堂灌”,课后布置几个与例题类似的习题,学生照猫画虎完成作业便大功告成。这种教学方式的弊端是,课堂缺乏生气,学生参与率不高。有相当一部分学生,或看小说,或睡觉,或聊天,或玩手机……,教学效果可想而知。
数学实验的教学方式是以学生操作为主,教师辅导为辅。在教学过程中,教师提出一些思考题目,甚至一些猜想,鼓励学生独立思考、勇于创新。学生可以自己选择实验题目,建立数学模型,在数学软件平台上编程、计算、分析结果等;学生也可以大胆地质疑某个数学原理或某个自然现象,通过自己或群体的讨论、分析,去论证结论的合理性。学生主动学习、合作讨论,教师启发引导、评价监督,这种开放式教学方式,充分利用了学生交流、研讨、相互促进的“群体效应”来提升教学效果,反映了以学生为中心的新理念。
因此,转变高等数学的课堂教学参与率不高的对策是,课堂转移到计算机机房,使课堂教学方式实验化。选择一种数学软件作为实验平台,通过教师的实验演示,向学生展示一个实验探究的课堂情境和氛围,使学生体会到有趣的思考过程;课堂作业甚至课后作业(有条件的话),都可以在实验平台上完成,真正实现学生主体、学生中心的地位。
(四)关于教学评价
传统的评价方式是在期末实行闭卷考试,考试题类似于例题。在这种评价方式下,出现了“高分低能”现象,以及对高等数学一知半解的学生竟能过关的奇怪现象。建议将高等数学考试分为闭卷和开卷两种方式,闭卷考试的内容注重基础知识和基本技能,重点考察基本概念、基本思想和方法,采用笔试形式,权重40%。开卷考试的内容注重考察数学探究和应用能力,重点考察数学理论的验证、复杂的运算,提出猜想、发现规律、数学建模与求解等。采用3人一组上机操作形式,在教师给定的参考题中选择1个题目进行实验,也可以自选题目,权重60%。
通过这种终结性评价和形成性评价相结合的评价方式,既考察了知识,又考察了能力;既重结果,更重过程。评价结果更全面,更客观。
(五)关于教材
教材是知识的载体。传统教材以知识为中心,注重学科体系的完整性,体现了知识发展的逻辑顺序。但是,作为教学用书的教材,必须体现学生中心和能力本位的思想。华东师范大学教授张奠周先生提出知识有三种形态:原始形态、学术形态和教育形态[1]。传统教材中的知识,是学术形态的知识,是精致美丽的成品,没有体现数学家探求知识的思维过程,学生读不出知识产生过程中的苦闷和乐趣。而数学实验的内容,富有生动的实验过程和直观的实验结果,充满了情趣,符合学生的学习心理特点。教材也应该进行实验化改造,将实验内容充实到教材中去,使教材面貌生动活泼,内容丰富多彩,学生学习从“实验”开始,学生会更喜欢。美国工业与应用数学学会(SIAM)教育委员会主席斯特朗(Strang)教授于1991年出版了新编“微积分”教材很有特色,强调了“数学思想”。在应用问题中,收录了心电图分析等生物数学以及不少经济管理中的问题。该书还介绍了当前发展很快的符号运算软件,并结合新一代袖珍计算器,介绍如何借助计算器实现计算和作图。这本书在美国好评如潮,引起数学教育界的轰动[2]。我们的教材改革也应该借鉴这种做法。
结论和建议
在高职院校实施数学实验课程的途径有两种:与高等数学异步交替式和选修课形式。高等数学与数学实验异步交替式教学,能够加深学生对数学知识的理解和巩固,增强数学兴趣,深化数学体验,增强创新精神,提高数学应用能力,养成用实验方法解决数学问题的习惯。
参考文献:
[1]张奠周.关于数学知识的教育形态[J].数学通报,2001,(5):2.
[2]段卫龙.强化数学实验教学,提高应用数学能力[J].数学理论与应用,2002,22(4):32
作者简介:
王积建(1966—),男,甘肃景泰人,讲师,硕士,主要从事高等数学教学和数学教育研究。
[1]