首页 -> 2007年第12期
高职院校数学建模活动的探索与实践
作者:凌巍炜
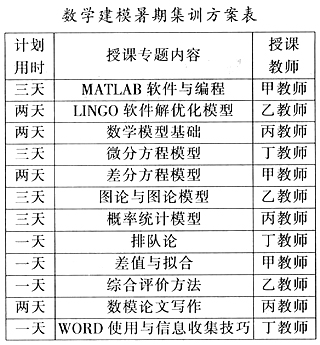
第三阶段为模拟实战与案例分析阶段。这一阶段主要选择历年真题对学生进行实战模拟,完全按照竞赛的实际要求,令学生在三天内交出论文。其目的是使学生在教练的论文点评与案例分析指导下,不断发现和改正存在的问题,全面提高建模水平,掌握应赛的必要技巧。除此之外,我们还强调如下几个方面:(1)加强学生对竞赛中各个环节的熟悉程度;(2)加强学生的团队精神和沟通能力、队员之间配合的默契程度;(3)加强学生对论文细节部分的处理能力;(4)加强对薄弱环节的训练。
(三)数学建模组赛
数学建模的组赛也是一项系统的工作,涉及方方面面和各个部门。
报名与队员选拔数学建模需要长期积累,因此,应尽早面向全校学生开展报名工作。报名工作一般安排在每学年的第二学期初进行,报名以学生自愿为主,数学任课教师推荐为辅,要求报名的学生具有较好的数学基础,有自我提高的要求,有较好的纪律性等。在学生自愿报名后,教练组要根据学生在校表现、高数课程的学习情况等,确定参加数学建模培训的学员,以降低培训中学员的流失率,选拔优秀学员。数学建模参赛队员的选拔直接关系到学校的参赛成绩,故选拔工作应该做到程序化,根据培训内容分多次进行。我校的做法是:在报名初期做一次初步筛选,入选的学生进入数学建模第一阶段的初级培训。第一阶段培训结束后,根据学员数学规划课程的成绩,选拔进入暑期集训的学员。暑期集训后,根据其建模能力和综合素质,选拔进入第三阶段培训的学员。最后,在第三阶段中期,根据学生模拟实战的表现情况最终确定参赛队员。
后勤保障培训期间,指导教师和培训学员都必须全身心投入其中;竞赛期间,学生除了吃饭以及少量的休息时间外,要把所有的精力全部放到建模上。这就要求有关部门有坚强的后勤保障,让教师和学生没有后顾之忧。在后勤保障方面,我校的做法是:由基础部负责具体实施,各相关部门大力配合,例如图书馆为参赛队员借书提供“绿色通道”,信息系提供专门机房供活动使用,宿管办为集训学生统一安排住宿等。为保证竞赛活动顺利进行,学院每年拨出专款为竞赛购置必要的设备及所需教材、资料等,为数学建模竞赛活动提供可靠的经费保证。竞赛期间,学院统一安排食宿,为每支参赛队伍配备三台计算机和打印机等。实践证明,我院取得的优异成绩与领导的重视、各部门的支持是分不开的。
以数学建模为切入点
推动高职数学教学改革
(一)以数学建模为切入点推动高职数学教学内容和教学方法的改革
目前,高职数学的教学内容基本沿袭了经典数学的三大块:微积分、线性代数、概率论与数理统计。这些内容都是单纯的数学理论,缺乏与实际问题的结合,并且游离于专业课之外,不仅不能引起学生的学习兴趣,而且也是专业系部压缩数学课时的因素之一。教师的教学方法也只是注重数学知识的灌输,教师讲解、教师设问、教师给出标准答案,只管教不管懂,这种常规的“填鸭”式教学方法很难调动学生学习数学的热情。
高职教育是培养高等应用型技术人才的教育。因此,高职数学的教学内容应充分体现“以应用为目的,以必需、够用为度”的原则,并将其作为专业课程的基础,强调其应用性以及解决实际问题的自觉性。一方面可以进一步扩大数学建模的受益面,有条件的情况下可以开设《数学建模》与《数学实验》课程,系统介绍数学建模的思想方法以及数学软件的使用方法;另一方面可以在高职数学教学中融入数学建模思想,将一些实际问题引入教学内容,利用一定的课时讲解浅易的数学建模,以增强数学内容的应用性、实践性、趣味性。在教学方法上,应注重理论联系实际,注重将数学的应用贯穿于教学始终,提倡“启发式”、“互动式”的教学模式,采用多媒体、数学实验等多种形式。
(二)以数学建模为切入点推动高职数学教学手段和教学工具的改革
随着现代科学技术的飞速发展,数学的应用领域日益广泛。数学建模的赛题都是一些经过适当简化加工的实际问题,这些问题为数学知识的应用提供了很好的实例。这些实例能使学生认识到数学如何有用,进而深入了解数学应用的方法和技巧。在数学建模中,为了求得模型的解,必须使用计算机和相关数学软件,数学应用与计算机已紧密结合。传统的教学手段——一支粉笔、一块黑板,已不适应数学的发展和应用,计算机进入数学教学势在必行。首先,可以在数学教学手段上引入多媒体教学,提高学生学习数学的兴趣;其次,在教学工具上引入数学软件求解数学问题,采用数学实验课的形式,促进数学与计算机的结合。
两点思考
目前,高职院校只有少数人参与数学建模活动,而且大部分高职院校只是为了竞赛而开展这项活动。对于如何扩大受益面的问题,本专科院校做了一些有益探索,比如开设数学实验课程或数学建模课程,但对于学制较短、职业性较强的高职院校来说,能否借鉴他们的经验开设选修课,如何开设并安排数学建模的教学内容等,仍是有待解决的课题。
数学建模提供的教学、培训模式和竞赛方式,在成绩较好的学生中取得了良好效果,但对于基础较差的学生却是一项高难度活动。因此,需要在实践过程中不断探索适用于高职院校所有学生的数学建模。
参考文献:
[1]叶其孝.大学生数学建模竞赛辅导教材(四)[M].长沙:湖南教育出版社,2002.
[2]何文阁.在高职院校开展数学建模活动的意义与实践[J] .中国职业技术教育,2005,(9):40.
[3]张纬民.对数学建模竞赛实施的点滴探索与认识[J].大学数学,2004,(3):33-34.
[4]李树冬.指导学生数学建模竞赛对数学教学改革的启示[J].上海商业职业技术学院学报,2004,(6):66-68.
[5]肖兆武.高职院校参加数学建模竞赛活动的探索[J].成人教育,2004,(6):60-61.
作者简介:
凌巍炜(1983—),男,江西应用技术职业学院教师,研究方向为数学建模、数学教学。
[1]